题目内容
3.动点P与定点F(6,0)的距离和它到定直线$x=\frac{2}{3}$的距离的比是3,求动点P的轨迹方程,并说明轨迹是什么图形.分析 设P(x,y)是轨迹上任意一点,依题意,$\frac{\sqrt{(x-6)^{2}+{y}^{2}}}{|x-\frac{2}{3}|}=3$,由此能求出点P的轨迹方程与点P的轨迹.
解答 解:设P(x,y)是轨迹上任意一点,
依题意,$\frac{\sqrt{(x-6)^{2}+{y}^{2}}}{|x-\frac{2}{3}|}=3$,
化简得点P的轨迹方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{32}$=1,
点P的轨迹是双曲线.
点评 本题考查点的轨迹方程的求法,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
15.“$\frac{1}{x}<\frac{1}{2}$”是“x>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
12.已知命题p:函数$y=sin\frac{π}{2}x$在x=a处取到最大值;命题q:直线x-y+2=0与圆(x-3)2+(y-a)2=8相切;则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
13.下面函数中在定义域内是奇函数和单调增函数的是( )
| A. | y=e-x-ex | B. | y=tanx | C. | y=x-3|x| | D. | y=ln(x+2)-ln(2-x) |
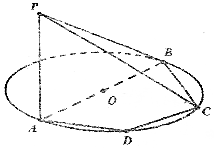 如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.
如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.