题目内容
19．某旅行社在暑假期间推出如下旅游团组团办法：达到100人的团体，每人收费1000元．如果团体的人数超过100人，那么每超过1人，每人平均收费降低5元，但团体人数不能超过180人，如何组团可使旅行社的收费最多？（不到100人不组团）分析 设有x人参加旅行团，收费共y元，由题意有y=1000x-5（x-100）x，（100≤x≤180）．由此能求出结果．
解答 解：设有x人参加旅行团，收费共y元，
则由题意有：
y=1000x-5（x-100）x，（100≤x≤180）．
整理函数关系式得：y=-5x2+1500x=-5（x-150）2+112500．
所以当x=150人时，旅行社的收费最多为112500元．
点评 本题考查函数在生产生活中的实际应用，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
9．直线xsinα+y+2=0的倾斜角的取值范围是（ ）
| A． | [0，π） | B． | [0，$\frac{π}{4}$]∪[$\frac{3}{4}$π，π） | C． | [0，$\frac{π}{4}$] | D． | [0，$\frac{π}{4}$]∪（$\frac{π}{2}$，π） |
10．集合P={x|（x-1）2＜4，x∈R}，Q={-1，0，1，2，3}，则P∩Q=（ ）
| A． | {0，1，2} | B． | {-1，0，1，2} | C． | {-1，0，2，3} | D． | {0，1，2，3} |
7．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|ω|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|ω|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（ ）| A． | 函数f（x）的最小正周期为2π | |
| B． | 函数f（x）的图象关于点（-$\frac{5π}{12}$.0）对称 | |
| C． | 将函数f（x）的图象向左平移$\frac{x}{6}$个单位得到的函数图象关于y轴对称 | |
| D． | 函数f（x）的单调递增区间是[kx+$\frac{7π}{12}$，kπ+$\frac{13π}{12}$]，（k∈Z） |
4．在棱长为1正方体ABCD-A1B1C1D1中，点E，F，G分别为DD1，BD，BB1的中点，则EF，CG所成角的余弦值为（ ）
| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{5}}}{15}$ | C． | $\frac{{\sqrt{15}}}{5}$ | D． | $\frac{{\sqrt{15}}}{15}$ |
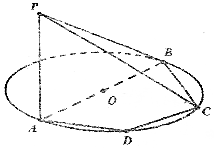如图，PA⊥⊙O面，PA=2，AB为⊙O的直径，其长为4，四边形ABCD内接于圆O，且∠ADC=120°．