题目内容
13.在△ABC中,若b2+c2-a2=bc,则角A的值为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 根据题中的等式,利用余弦定理算出cosA=$\frac{1}{2}$,结合0°<A<180°可得A=60°.
解答 解:∵在△ABC中,b2+c2-a2=bc,
∴根据余弦定理,得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$,
又∵0°<A<180°,
∴A=60°.
故选:B.
点评 本题给出三角形的三边的平方关系,求角A的大小.着重考查了利用余弦定理解三角形的知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在棱长为1正方体ABCD-A1B1C1D1中,点E,F,G分别为DD1,BD,BB1的中点,则EF,CG所成角的余弦值为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{15}}}{15}$ |
18.函数y=2sinx的定义域为[a,b],值域为[-2,$\sqrt{3}$],则b-a的最大值和最小值之和等于( )
| A. | 4π | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
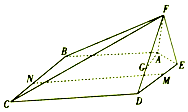 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.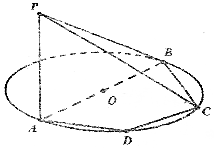 如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.
如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.