题目内容
13.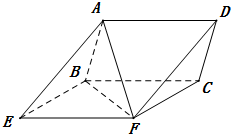 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.(Ⅰ)证明:AE⊥BF;
(Ⅱ)若∠BEF=60°,AE=$\sqrt{2}$AB=2,求三棱柱ABE-DFC的体积.
分析 (I)连接EC,与BF相交于点O,连接AO.由平行四边形的性质可得点O是BF的中点,利用等腰三角形的性质可得OA⊥BF,EO⊥BF,即可证明BF⊥平面AEO,即可得出AE⊥BF.
(II)由∠BEF=60°,BE=EF=2,可得△BEF是等边三角形,可得AB2+AF2=BF2,∠BAF=90°.可得OA2+OE2=AE2,由(I)可得:BF⊥平面AEO,于是VA-BEF=$\frac{1}{3}×{S}_{OAE}×BF$.可得三棱柱ABE-DFC的体积=3VA-BEF.
解答 (I)证明:连接EC,与BF相交于点O,连接AO.
∵四边形BEFC是平行四边形,
∴点O是BF的中点,
∵ AB=AF,BE=EF=2.
AB=AF,BE=EF=2.
∴OA⊥BF,EO⊥BF,
又OA∩OE=O,
∴BF⊥平面AEO,AE?平面OAE.
∴AE⊥BF.
(II)解:∵∠BEF=60°,BE=EF=2,
∴△BEF是等边三角形,
∴BF=2,OE=$\sqrt{3}$.
∵AE=$\sqrt{2}$AB=2,∴AB=$\sqrt{2}$=AF,
∴AB2+AF2=BF2,∴∠BAF=90°.
∴OA=OB=OF=1.
∴OA2+OE2=AE2,∴∠AOE=90°.
由(I)可得:BF⊥平面AEO,
∴VA-BEF=$\frac{1}{3}×{S}_{OAE}×BF$=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{3}$×2=$\frac{\sqrt{3}}{3}$.
∴三棱柱ABE-DFC的体积=3VA-BEF=$\sqrt{3}$.
点评 本题考查了三棱锥的体积计算公式及其性质、勾股定理及其逆定理、等腰与等边三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.下列各组对象能构成集合的有( )
①美丽的小鸟;
②不超过10的非负整数;
③立方接近零的正数;
④高一年级视力比较好的同学.
①美丽的小鸟;
②不超过10的非负整数;
③立方接近零的正数;
④高一年级视力比较好的同学.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.双曲线$\frac{x^2}{m+1}$+$\frac{y^2}{1-2m}$=1的焦点在y轴上,则m的取值范围是( )
| A. | m<-1 | B. | $-1<m<\frac{1}{2}$ | C. | $m<\frac{1}{2}$ | D. | $m>\frac{1}{2}$ |