题目内容
3.已知集合E={x||x-1|≥m},F=$\{x|\frac{10}{x+6}>1\}$.(1)若m=3,求E∩F;
(2)若E∩F=∅,求实数m的取值范围.
分析 (1)m=3时求出集合E,化简集合F,计算E∩F即可;
(2)由E∩F=∅,得出关于m的不等式组,从而求出m的取值范围.
解答 解:(1)由|x-1|≥3,得 x-1≥3或x-1≤-3,
解得x≥4或x≤-2,
所以 E=(-∞,-2]∪[4,+∞);
由$\frac{10}{x+6}$-1>0,得$\frac{10-x-6}{x+6}$>0;
即(x-4)(x+6)<0,
解得-6<x<4;
所以F=(-6,4);
所以E∩F=(-6,-2];
(2)E∩F=∅,
则有m>0,E=(-∞,1-m]∪[1+m,+∞),
即$\left\{{\begin{array}{l}{1-m≤-6}\\{1+m≥4}\end{array}}\right.$,
解得$\left\{\begin{array}{l}{m≥7}\\{m≥3}\end{array}\right.$,
所以实数m的取值范围是m≥7.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
相关题目
12.直线$\sqrt{3}$x+3y+a=0的倾斜角为( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
9.《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
| A. | $\frac{8}{29}$尺 | B. | $\frac{16}{29}$尺 | C. | $\frac{32}{29}$尺 | D. | $\frac{1}{2}$尺 |
16.已知函数y=f(x)是函数y=3x的反函数,则$f({\frac{1}{9}})$=( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
12.执行如图所示的程序框图,输出的结果是( )


| A. | 65 | B. | 45 | C. | 55 | D. | 34 |
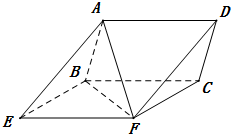 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.