题目内容
18.已知常数a>0,函数f(x)=ln(1+ax)-$\frac{2x}{x+2}$.讨论f(x)在区间(0,+∞)上的单调性.分析 利用导数判断函数的单调性,注意对a分类讨论.
解答 解:∵f(x)=ln(1+ax)-$\frac{2x}{x+2}$,
∴f′(x)=$\frac{a}{1+ax}$-$\frac{4}{{(x+2)}^{2}}$=$\frac{{ax}^{2}-4(1-a)}{(1+ax{)(x+2)}^{2}}$,
∵(1+ax)(x+2)2>0,
∴当1-a≤0时,即a≥1时,f′(x)≥0恒成立,
则函数f(x)在(0,+∞)单调递增,
当0<a≤1时,由f′(x)=0得x=±$\frac{2\sqrt{a(1-a)}}{a}$,
则函数f(x)在(0,$\frac{2\sqrt{a(1-a)}}{a}$)单调递减,在($\frac{2\sqrt{a(1-a)}}{a}$,+∞)单调递增.
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.f:x→x2是集合A到集合B的映射,如果B={1,2},那么A∩B只可能是( )
| A. | {1,2} | B. | {1}或∅ | C. | $\left\{{1,\sqrt{2},2}\right\}$ | D. | {1} |
3.函数f(x)=$\frac{1}{\sqrt{2x-3}}$的定义域是( )
| A. | (0,$\frac{3}{2}$) | B. | [$\frac{3}{2}$,+∞) | C. | (-∞,$\frac{3}{2}$] | D. | ($\frac{3}{2}$,+∞) |
10.下列判断错误的是( )
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| C. | 命题“?x∈R,ax+b≤0”的否定是“?x∈R,ax+b>0” | |
| D. | 若ξ~B(8,0.125),则Eξ=1 |
7.函数f(x)=x3-3|x|+1(x≤1)的零点所在区间为( )
| A. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{2},1)$ | B. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{3},\frac{1}{2})$ | C. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{2},1)$ | D. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{3},\frac{1}{2})$ |
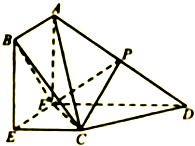 如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.
如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.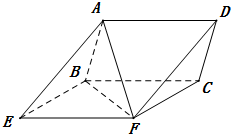 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.