题目内容
4.已知椭圆C过点A(1,$\frac{3}{2}$),两个焦点为F1(-1,0),F2(1,0).求椭圆C的方程及离心率.分析 由题意可知:椭圆的焦点在x轴上,且c=1,设设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-1}=1$,(a>1),将A(1,$\frac{3}{2}$)代入椭圆方程,即可求得a的值,求得椭圆方程,由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$.
解答 解:由题意可知:焦点为F1(-1,0),F2(1,0),椭圆的焦点在x轴上,c=1,
则设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-1}=1$,(a>1),将A(1,$\frac{3}{2}$)代入椭圆方程,
则$\frac{1}{{a}^{2}}+\frac{9}{4({a}^{2}-1)}$=1,4a4-17a2+4=0,解得:a2=$\frac{1}{4}$,a2=4,
由a>1,
∴a2=4,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,
由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,
∴椭圆C的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,离心率$\frac{1}{2}$.
点评 本题考查椭圆的标准方程及简单几何性质,考查椭圆的离心率公式,考查计算能力,属于基础题.

练习册系列答案
相关题目
12.直线$\sqrt{3}$x+3y+a=0的倾斜角为( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
12.执行如图所示的程序框图,输出的结果是( )


| A. | 65 | B. | 45 | C. | 55 | D. | 34 |
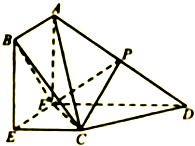 如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.
如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.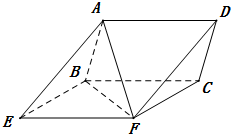 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.