题目内容
8.若函数f(x)=$\left\{\begin{array}{l}{x^2}+1(x>0)\\ π(x=0)\\ 0(x<0)\end{array}$,则f(f(f(-2016)))=π2+1.分析 由已知得f(-2016)=0,从而f(f(-2016))=f(0)=π,进而f(f(f(-2016)))=f(π),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{x^2}+1(x>0)\\ π(x=0)\\ 0(x<0)\end{array}$,
∴f(-2016)=0,
f(f(-2016))=f(0)=π,
f(f(f(-2016)))=f(π)=π2+1.
故答案为:π2+1.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
16.已知函数y=f(x)是函数y=3x的反函数,则$f({\frac{1}{9}})$=( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
3.下列四组函数中,表示为同一函数的是( )
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | B. | y=x0与g(x)=$\frac{1}{{x}^{0}}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
17.若集合P={x|log2x<2},Q={1,2,3},则P∩Q=( )
| A. | {1,2} | B. | {1} | C. | {2,3} | D. | {1,2,3} |
18.在正项数列{an}中,a1=2,且点($\sqrt{a_n}$,$\sqrt{{a_{n-1}}}$)在直线x-$\sqrt{2}$y=0上,则前n项和Sn等于( )
| A. | 2n-1 | B. | 2n+1-2 | C. | ${2^{\frac{n}{2}}}-\sqrt{2}$ | D. | ${2^{\frac{n-2}{2}}}-\sqrt{2}$ |
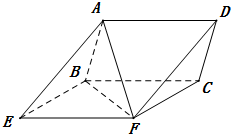 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.