题目内容
5.数列{an}中,a1=1,an+1=an+2(n∈N*),求a8的值.分析 由题意,得到数列是首项为1,公差为2的等差数列,
解答 解:由已知递推关系得到数列是首项为1,公差为2的等差数列,所以a8=a1+7d=1+2×7=15.
点评 本题考查了等差数列的定义运用;关键是由递推关系得到数列是等差数列.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
10.下列判断错误的是( )
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| C. | 命题“?x∈R,ax+b≤0”的否定是“?x∈R,ax+b>0” | |
| D. | 若ξ~B(8,0.125),则Eξ=1 |
17.若集合P={x|log2x<2},Q={1,2,3},则P∩Q=( )
| A. | {1,2} | B. | {1} | C. | {2,3} | D. | {1,2,3} |
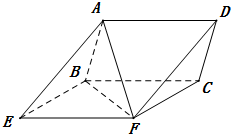 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.