题目内容
2.双曲线$\frac{x^2}{m+1}$+$\frac{y^2}{1-2m}$=1的焦点在y轴上,则m的取值范围是( )| A. | m<-1 | B. | $-1<m<\frac{1}{2}$ | C. | $m<\frac{1}{2}$ | D. | $m>\frac{1}{2}$ |
分析 由题意可得1-2m>0,且m+1<0,解不等式即可得到m的范围.
解答 解:双曲线$\frac{x^2}{m+1}$+$\frac{y^2}{1-2m}$=1的焦点在y轴上,
可得1-2m>0,且m+1<0,
即m<$\frac{1}{2}$,且m<-1,
则m的取值范围是m<-1.
故选:A.
点评 本题考查双曲线方程和性质,考查不等式的解法,属于基础题.

练习册系列答案
相关题目
12.执行如图所示的程序框图,输出的结果是( )


| A. | 65 | B. | 45 | C. | 55 | D. | 34 |
10.下列判断错误的是( )
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| C. | 命题“?x∈R,ax+b≤0”的否定是“?x∈R,ax+b>0” | |
| D. | 若ξ~B(8,0.125),则Eξ=1 |
17.若集合P={x|log2x<2},Q={1,2,3},则P∩Q=( )
| A. | {1,2} | B. | {1} | C. | {2,3} | D. | {1,2,3} |
7.函数f(x)=x3-3|x|+1(x≤1)的零点所在区间为( )
| A. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{2},1)$ | B. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{3},\frac{1}{2})$ | C. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{2},1)$ | D. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{3},\frac{1}{2})$ |
12.△ABC中,B=45°,b=x,a=2,若△ABC有两解,则x的取值范围是( )
| A. | (2,+∞) | B. | (0,2) | C. | (2,2$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
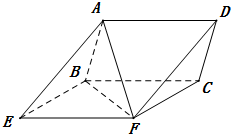 如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.
如图所示的三棱柱ABE-DCF中,AB=AF,BE=EF=2.