题目内容
已知函数f（x）=
，若k＞0，则方程|f（x）|-1=0的解个数有 ．
|
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：将方程的解的问题转化为函数的交点问题，画出函数图象一目了然．
解答：
解：画出函数y=|f（x）|的图象，
如图示：
，
∴方程|f（x）|-1=0的解有4个，
故答案为：4个．
如图示：
，∴方程|f（x）|-1=0的解有4个，
故答案为：4个．
点评：本题考查了方程的根的存在性问题，考查转化思想，是一道基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
下列三视图表示的几何体是（ ）
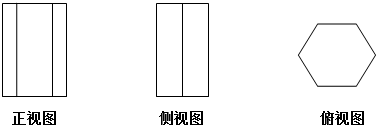
| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |
设θ∈（
，π），则关于x，y的方程
+
=1所表示的曲线为（ ）
| 3π |
| 4 |
| x2 |
| sinθ |
| y2 |
| cosθ |
| A、长轴在y轴上的椭圆 |
| B、长轴在x轴上的椭圆 |
| C、实轴在y轴上的双曲线 |
| D、实轴在x轴上的双曲线 |
4张卡片上分别写有数字1，2，3，4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|