题目内容
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5.同时投掷这两枚玩具一次,记m为两个下的面上的数字之和.
(Ⅰ)求事件“m不小于6”的概率;
(Ⅱ)求事件“m为奇数”的概率.
(Ⅰ)求事件“m不小于6”的概率;
(Ⅱ)求事件“m为奇数”的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(Ⅰ)根据题意,由列举法可得基本事件的情况,可得其情况数目,分析可得事件“m不小于6”包含的基本事件数目,由等可能事件的概率公式计算可得答案;
(Ⅱ)根据题意,分析可得m为奇数有3种情况,即m=3、m=5与m=7;由(1)的列举结果可得m=3、m=5与m=7的情况数目,由等可能事件的概率公式可得m为奇数的情况数目,
(Ⅱ)根据题意,分析可得m为奇数有3种情况,即m=3、m=5与m=7;由(1)的列举结果可得m=3、m=5与m=7的情况数目,由等可能事件的概率公式可得m为奇数的情况数目,
解答:
解:( I)同时投掷这两枚玩具的结果有
(1,1),(1,2),(1,3),(1,5)
(2,1),(2,2),(2,3),(2,5)
(3,1),(3,2),(3,3),(3,5)
(5,1),(5,2),(5,3),(5,5)共16种
记事件“m不小于6”为事件A,
有(1,5),(2,5),(3,3),(3,5),(5,1),(5,2),(5,3),(5,5),8个基本事件,
∴P(A)=
=
(Ⅱ)m为奇数有3种情况,即m=3、m=5与m=7;
m=3的情况有(1,2)、(2,1),共2种,
m=5的情况有(2,3)、(3,2),共2种,
m=7的情况有(2,5)、(5,2),共2种,
记事件“m为奇数”的概率B,共有6个,
∴P(B)=
=
(1,1),(1,2),(1,3),(1,5)
(2,1),(2,2),(2,3),(2,5)
(3,1),(3,2),(3,3),(3,5)
(5,1),(5,2),(5,3),(5,5)共16种
记事件“m不小于6”为事件A,
有(1,5),(2,5),(3,3),(3,5),(5,1),(5,2),(5,3),(5,5),8个基本事件,
∴P(A)=
| 8 |
| 16 |
| 1 |
| 2 |
(Ⅱ)m为奇数有3种情况,即m=3、m=5与m=7;
m=3的情况有(1,2)、(2,1),共2种,
m=5的情况有(2,3)、(3,2),共2种,
m=7的情况有(2,5)、(5,2),共2种,
记事件“m为奇数”的概率B,共有6个,
∴P(B)=
| 6 |
| 18 |
| 3 |
| 8 |
点评:本题考查等可能事件的概率计算,解题的关键是正确运用列举法,分析得到基本事件的情况数目

练习册系列答案
相关题目
已知f(x)是奇函数,当x>0时f(x)=-x(1+x),当x<0时,f(x)等于( )
| A、-x(1-x) |
| B、x(1-x) |
| C、-x(1+x) |
| D、x(1+x) |
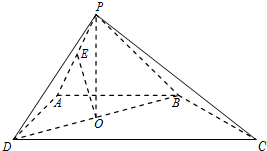 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.