题目内容
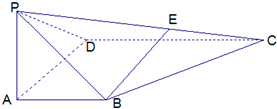
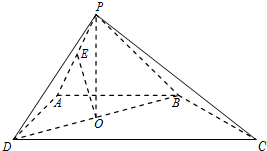 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.(Ⅰ)求证:OE∥平面PCD;
(Ⅱ)求直线CE与平面PDC所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取CD中点F,连BF,AF,PF,只要证明OE∥PF;
(2)首先判断PO⊥平面ABCD,建立坐标系,利用线面角的正弦值转化为直线的方向向量与平面的法向量的余弦值解答.
(2)首先判断PO⊥平面ABCD,建立坐标系,利用线面角的正弦值转化为直线的方向向量与平面的法向量的余弦值解答.
解答:
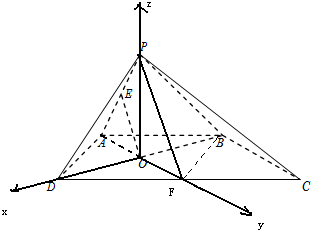 (Ⅰ)证明:取CD中点F,连BF,AF,PF,∴AB=DF,∵AB∥DF,∴四边形ADFB是平行四边形,∴AF∩BD=O,且O为AF中点,
(Ⅰ)证明:取CD中点F,连BF,AF,PF,∴AB=DF,∵AB∥DF,∴四边形ADFB是平行四边形,∴AF∩BD=O,且O为AF中点,
∴OE∥PF,PF?平面PCD,OE?平面PCD,∴OE∥平面PCD;
(Ⅱ)∵平行四边形ADFB中,AB=AD=2,AB⊥AD,∴四边形ADFB是正方形,
∴OD⊥OF,又PB=PD=2,O为BD的中点,
∴PO⊥OD,
同理PO⊥AF,
∴PO⊥平面ABCD,
分别以OD,OF,OP为x轴,y轴,z轴建立空间直角坐标系,如图
可得平面PDC的一个法向量为
=(1,1,1),
=(
,-
,
),所以直线CE的一个方向向量为
=(2,-5,1),
设所求线面角为θ,所以sinθ=|cos<
,
>|=
=
;
所以直线CE与平面PDC所成角的正弦值为
.
 (Ⅰ)证明:取CD中点F,连BF,AF,PF,∴AB=DF,∵AB∥DF,∴四边形ADFB是平行四边形,∴AF∩BD=O,且O为AF中点,
(Ⅰ)证明:取CD中点F,连BF,AF,PF,∴AB=DF,∵AB∥DF,∴四边形ADFB是平行四边形,∴AF∩BD=O,且O为AF中点,∴OE∥PF,PF?平面PCD,OE?平面PCD,∴OE∥平面PCD;
(Ⅱ)∵平行四边形ADFB中,AB=AD=2,AB⊥AD,∴四边形ADFB是正方形,
∴OD⊥OF,又PB=PD=2,O为BD的中点,
∴PO⊥OD,
同理PO⊥AF,
∴PO⊥平面ABCD,
分别以OD,OF,OP为x轴,y轴,z轴建立空间直角坐标系,如图
可得平面PDC的一个法向量为
| n |
| CE |
| 2 |
5
| ||
| 2 |
| ||
| 2 |
| a |
设所求线面角为θ,所以sinθ=|cos<
| n |
| a |
|
| ||||
|
|
| ||
| 15 |
所以直线CE与平面PDC所成角的正弦值为
| ||
| 15 |
点评:本题考查了线面平行以及线面角的求法,线面平行的判断关键是转化为线线平行证明;线面角的正弦值转化为直线的方向向量与平面的法向量的余弦值解答,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合A={x|x2-3x<0},集合B={y|y=2x,0≤x≤1},则A∩B=( )
| A、(0,1] |
| B、(0,2] |
| C、[1,2] |
| D、[1,3) |
若一条直线与两个平行平面中的一个平面平行,则这条直线与另一个平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
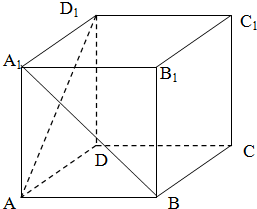 已知正方体ABCD-A1B1C1D1,求:
已知正方体ABCD-A1B1C1D1,求: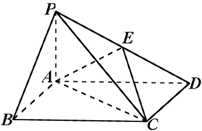 如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=3,且三棱锥E-ACD的体积为1.
如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=3,且三棱锥E-ACD的体积为1.