题目内容
(1)求直线x-y+4=0被圆(x+2)2+(y-2)2=2截得的弦长.
(2)直线x-2y-3=0与圆(x-2)2+(y+3)2=9交于E,F两点,求△EOF(O是原点)的面积.
(2)直线x-2y-3=0与圆(x-2)2+(y+3)2=9交于E,F两点,求△EOF(O是原点)的面积.
考点:直线与圆相交的性质
专题:直线与圆
分析:(1)利用用圆心到直线的距离来求解.
(2)先求出圆心坐标,再由点到直线的距离公式和勾股定理求出弦长|EF|,再由原点到直线之间的距离求出三角形的高,进而根据三角形的面积公式求得答案.
(2)先求出圆心坐标,再由点到直线的距离公式和勾股定理求出弦长|EF|,再由原点到直线之间的距离求出三角形的高,进而根据三角形的面积公式求得答案.
解答:
解:(1)圆心为(-2,2),半径为
,
圆心到直线x-y+4=0的距离为d=
=0,
故|AB|=2
.
(2)圆(x-2)2+(y+3)2=9的圆心为(2,-3)
∴(2,-3)到直线x-2y-3=0的距离d=
=
=
弦长|EF|=2
=2
=4
原点到直线的距离d=
=
,
∴△EOF的面积为S=
×4×
=
.
| 2 |
圆心到直线x-y+4=0的距离为d=
| |-2-2+4| | ||
|
故|AB|=2
| 2 |
(2)圆(x-2)2+(y+3)2=9的圆心为(2,-3)
∴(2,-3)到直线x-2y-3=0的距离d=
| |2-2×(-3)-3| | ||
|
| 5 | ||
|
| 5 |
弦长|EF|=2
| R2-d2 |
| 9-5 |
原点到直线的距离d=
| |-3| | ||
|
3
| ||
| 5 |
∴△EOF的面积为S=
| 1 |
| 2 |
3
| ||
| 5 |
6
| ||
| 5 |
点评:本题主要考查点到直线的距离公式和直线与圆的位置关系.考查基础知识的综合运用和灵活运用能力.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
若一条直线与两个平行平面中的一个平面平行,则这条直线与另一个平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
一个与球心距离为1的平面截球所得的圆面面积为4π,则球的表面积为( )
| A、5π | B、17π |
| C、20π | D、68π |
不等式x(x-1)<0的解集是( )
| A、{x|x<0} |
| B、{x|x<1} |
| C、{x|0<x<1} |
| D、{x|x<0或x>1} |
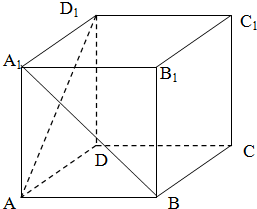 已知正方体ABCD-A1B1C1D1,求:
已知正方体ABCD-A1B1C1D1,求: