题目内容
4．设函数f（x）=1n（1+e-2x），则f′（0）=-1．分析 先利用差的导数运算法则求出f（x）的导函数，令导函数中的x等于0求出f′（0）的值．
解答 解：f′（x）=$\frac{1}{1+{e}^{-2x}}$（1+e-2x）′=$\frac{1}{1+{e}^{-2x}}$•（-2e-2x），
∴f′（0）=$\frac{1}{1+1}$•（-2）=-1，
故答案为：-1．
点评 求函数在某点处的导数值，应该先求出函数的导函数，再求导函数值．
练习册系列答案
相关题目
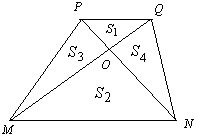如图，在梯形PMNQ中，PQ∥MN，对角线PN和MQ相交于点O，并把梯形分成四部分，记这四部分的面积分别为S1，S2，S3，S4．试判断S1+S2和S3+S4的大小关系，并证明你的结论．
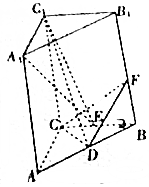如图，三棱柱ABC-A1B1C1中，CC1⊥平面ABC，∠ACB=90°，BB1=3，AC=BC=2，D，E分别为AB，BC的中点，F为BB1上一点，且$\frac{BF}{F{B}_{1}}$=$\frac{2}{7}$．