题目内容
9.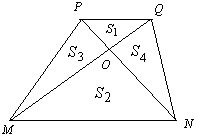 如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.
如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.
分析 设PQ=m,MN=n,根据同底等判断S△PMN=S△QMN,再根据三角形面积的相似比,即可用,m,n表示出S1,S2,S3,S4.再利用作差法比较大小即可.
解答 解:设PQ=m,MN=n,
∵△PMN和△QMN同底等高,
∴S△PMN=S△QMN,
∴S3+S2=S4+S2,即:S3=S4.
∵△POQ∽△NOM,
∴${S_1}:{S_2}={(OQ:OM)^2}={m^2}:{n^2}$,
∴${S_2}=\frac{n^2}{m^2}•{S_1}$.
∵S1:S3=OQ:OM=m:n,
∴${S_3}=\frac{n}{m}•{S_1}$.
∴(S1+S2)-(S3+S4)=S1+$\frac{{n}^{2}}{{m}^{2}}$+S2-2•$\frac{n}{m}$S1=S1(1+$\frac{{n}^{2}}{{m}^{2}}$-$\frac{2n}{m}$)=S1(1-$\frac{n}{m}$)2.
∵${(1-\frac{n}{m})^2}>0$,
∴S1+S2>S3+S4.
点评 本题考查了相似三角形的性质,以及作差法比较大小,属于中档题.

练习册系列答案
相关题目
19.抛物线y=x2-4x+3与x轴围成的封闭图形的面积为( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
20.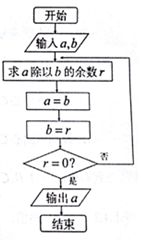 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法-“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a=3051,b=1008时,输出的a=( )
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法-“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a=3051,b=1008时,输出的a=( )
 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法-“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a=3051,b=1008时,输出的a=( )
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法-“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a=3051,b=1008时,输出的a=( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
4.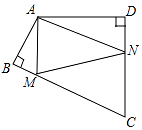 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |