题目内容
4.已知数列{an}的前n项和为Sn,a1=a,${a_2}={a^2}$,an+2=an+1-an,S56=6,则a=-3或2.分析 由an+1=an-an-1(n≥2),得an+6=an+5-an+4=an+4-an+3-an+4=-an+3=-(an+2-an+1)=-(an+1-an-an+1)=an,所以6为数列{an}的周期,可得S6=0.于是S56=S54+a+a2=a+a2=6,解得a.
解答 解:由an+1=an-an-1(n≥2),得
an+6=an+5-an+4=an+4-an+3-an+4=-an+3=-(an+2-an+1)=-(an+1-an-an+1)=an,
所以6为数列{an}的周期,
又a3=a2-a1=a2-a,a4=a3-a2=-a,a5=a4-a3=-a2,a6=a5-a4=a-a2,
∴S6=0.
∵S56=6,∴S56=S54+a+a2=a+a2=6,解得a=-3或2.
故答案为:-3或2.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
19.抛物线y=x2-4x+3与x轴围成的封闭图形的面积为( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
9.设a,b∈R,i是虚数单位,则“$a=\sqrt{3}$,b=1”是“$|{\frac{1+bi}{a+i}}|=\frac{{\sqrt{2}}}{2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
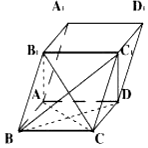 如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形,侧面A1ABB1⊥底面ABCD,AA1=2,∠B1BA=30°.
如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形,侧面A1ABB1⊥底面ABCD,AA1=2,∠B1BA=30°.