题目内容
已知函数f(x)=|x+3|,g(x)=m-2|x-11|,若2f(x)≥g(x+4)恒成立,实数m的最大值为t.
(1)求实数m.
(2)已知实数x、y、z满足2x2+3y2+6z2=a(a>0),且x+y+z的最大值是
,求a的值.
(1)求实数m.
(2)已知实数x、y、z满足2x2+3y2+6z2=a(a>0),且x+y+z的最大值是
| t |
| 20 |
考点:绝对值不等式的解法,二维形式的柯西不等式
专题:不等式的解法及应用
分析:(1)若2f(x)≥g(x+4)恒成立,可得m≤2(|x+3|+|x-7|),而由绝对值三角不等式可得 2(|x+3|+|x-7|)≥20,可得m≤20,由此求得m的最大值t.
(2)由柯西不等式可得[(
x)2+(
y)2+(
z)2]•[(
)2+(
)2+(
)2]≥(
x•
+
y•
+
z•
)2,即a×1≥(x+y+z)2,即x+y+z≤
.再根据 x+y+z的最大值是
=1,可得
=1,从而求得a的值.
(2)由柯西不等式可得[(
| 2 |
| 3 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 1 | ||
|
| 3 |
| 1 | ||
|
| 6 |
| 1 | ||
|
| a |
| t |
| 20 |
| a |
解答:
解:(1)由题意可得g(x+4)=m-2|x+4-11|=m-2|x-7|,若2f(x)≥g(x+4)恒成立,
∴2|x+3|≥m-2|x-7|,即 m≤2(|x+3|+|x-7|).
而由绝对值三角不等式可得 2(|x+3|+|x-7|)≥2|(x+3)-(x-7)|=20,
∴m≤20,故m的最大值t=20.
(2)∵实数x、y、z满足2x2+3y2+6z2=a(a>0),由柯西不等式可得
[(
x)2+(
y)2+(
z)2]•[(
)2+(
)2+(
)2]≥(
x•
+
y•
+
z•
)2.
∴a×1≥(x+y+z)2,∴x+y+z≤
.
再根据 x+y+z的最大值是
=1,∴
=1,∴a=1.
∴2|x+3|≥m-2|x-7|,即 m≤2(|x+3|+|x-7|).
而由绝对值三角不等式可得 2(|x+3|+|x-7|)≥2|(x+3)-(x-7)|=20,
∴m≤20,故m的最大值t=20.
(2)∵实数x、y、z满足2x2+3y2+6z2=a(a>0),由柯西不等式可得
[(
| 2 |
| 3 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 1 | ||
|
| 3 |
| 1 | ||
|
| 6 |
| 1 | ||
|
∴a×1≥(x+y+z)2,∴x+y+z≤
| a |
再根据 x+y+z的最大值是
| t |
| 20 |
| a |
点评:本题主要考查绝对值三角不等式、柯西不等式的应用,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
执行如图所示的程序框图,若输出的值为-105,则输入的n值可能为( )

| A、5 | B、7 | C、8 | D、10 |
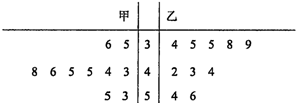
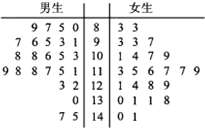 某校高三年级从一次模拟考试中随机抽取50名学生(男、女各25名),将数学成绩进行统计,所得数据的茎叶图如图所示.其中成绩在120分以上(含120分)为优秀.
某校高三年级从一次模拟考试中随机抽取50名学生(男、女各25名),将数学成绩进行统计,所得数据的茎叶图如图所示.其中成绩在120分以上(含120分)为优秀.