Question

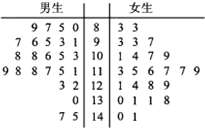某校高三年级从一次模拟考试中随机抽取50名学生（男、女各25名），将数学成绩进行统计，所得数据的茎叶图如图所示．其中成绩在120分以上（含120分）为优秀．
（1）根据茎叶图估计这次模拟考试女生成绩的中位数；
（2）根据茎叶图完成2×2列联表：能否有85%的把握认为成绩优秀与性别有关？

	成绩不优秀	成绩优秀	总数
男生
女生
总数

参考公式：独立性检验K²=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

P（K2≥k）	0.25	0.15	0.10	0.05
k	1.323	2.072	2.706	3.841

Answer 1

考点：独立性检验的应用

专题：计算题,概率与统计

分析：（1）由茎叶图可知女生成绩的中位数为117分，从而估计这次模拟考试女生成绩的中位数；
（2）根据茎叶图，可得2×2列联表，由列联表中数据，代入公式，求出K²的值，进而与2.072进行比较，即可得出能否有85%的把握认为环保知识测试成绩与专业有关．

解答： 解：（1）由茎叶图可知女生成绩的中位数为117分，
∴估计这次模拟考试女生成绩的中位数为117分；
（2）根据茎叶图，可得2×2列联表

	成绩不优秀	成绩优秀	总数
男生	20	5	25
女生	15	10	25
总数	35	15	50

K²=50（20×10-15×5）²÷（25×25×35×15）≈2.381＞2.072，
∴有85%的把握认为成绩优秀与性别有关．

点评：本题考查独立性检验的应用，考查数据处理能力、运算求解能力和应用意识，本题解题的关键是正确运算出观测值，理解临界值对应的概率的意义，要想知道两个变量之间的有关或无关的精确的可信程度，只有利用独立性检验的有关计算，才能做出判断，本题是一个基础题．