题目内容
已知椭圆C:
+
=1(a>b>0)经过点D(2,0),E(1,
)两点.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m与椭圆C交于不同两点A,B,点G是线段AB的中点,点O为坐标原点,设射线OG交椭圆C于点Q,且
=λ
.
①证明:λ2m2=4k2+1;
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)若直线l:y=kx+m与椭圆C交于不同两点A,B,点G是线段AB的中点,点O为坐标原点,设射线OG交椭圆C于点Q,且
| OQ |
| OG |
①证明:λ2m2=4k2+1;
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆方程.
(2)①令A(x1,y1),B(x2,y2),由
,得(1+4k2)x2+8kmx+4m2-4=0,由此利用根的判别式、韦达定理、中点坐标公式、向量知识,结合已知条件能证明λ2m2=4k2+1.
②由|x1-x2|=
=
,S△AOB=
|m||x1-x2|,得S(λ)=
=
,λ>1,由此利用换元法能求出当λ=
时,S(λ)=
取得最大值1.
|
(2)①令A(x1,y1),B(x2,y2),由
|
②由|x1-x2|=
(
|
4
| ||
| 1+4k2 |
| 1 |
| 2 |
2|m|
| ||
| λ2m2 |
2
| ||
| λ2 |
| 2 |
2
| ||
| λ2 |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)经过点D(2,0),E(1,
)两点,
∴
,
解得a=2,b=1,
∴椭圆方程为
+y2=1.
(2)①证明:令A(x1,y1),B(x2,y2),
由
,消去y,得(1+4k2)x2+8kmx+4m2-4=0,
∴
,即
,
∴y1+y2=k(x1+x2)+2m=
+2m=
,
又由中点坐标公式,得G(
,
),
根据
=λ
,得Q(
,
),
将其代入椭圆方程,有
+
=1,
化简得:λ2m2=4k2+1.
②解:由①得m≠0,λ>1,
∵|x1-x2|=
=
,
在△AOB中,S△AOB=
|m||x1-x2|,
∴S(λ)=
=
,λ>1,
令
=t,t>0,
则S=
=
<
=1(当且仅当t=1时,即λ=
时取“=”)
∴当λ=
时,S(λ)=
取得最大值,其最大值为1.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
解得a=2,b=1,
∴椭圆方程为
| x2 |
| 4 |
(2)①证明:令A(x1,y1),B(x2,y2),
由
|
∴
|
|
∴y1+y2=k(x1+x2)+2m=
| k(-8km) |
| 1+4k2 |
| 2m |
| 1+4k2 |
又由中点坐标公式,得G(
| -4km |
| 1+4k2 |
| m |
| 1+4k2 |
根据
| OQ |
| OG |
| -4λkm |
| 1+4k2 |
| λm |
| 1+4k2 |
将其代入椭圆方程,有
| 4λ2k2m2 |
| (1+4k2)2 |
| λ2m2 |
| (1+4k2)2 |
化简得:λ2m2=4k2+1.
②解:由①得m≠0,λ>1,
∵|x1-x2|=
(
|
4
| ||
| 1+4k2 |
在△AOB中,S△AOB=
| 1 |
| 2 |
∴S(λ)=
2|m|
| ||
| λ2m2 |
2
| ||
| λ2 |
令
| λ2-1 |
则S=
| 2t |
| t2+1 |
| 2 | ||
t+
|
| 2 | ||
2
|
| 2 |
∴当λ=
| 2 |
2
| ||
| λ2 |
点评:本题考查椭圆C的方程的求法,考查λ2m2=4k2+1的证明,考查△AOB的面积S(λ)的解析式的求法,考查S(λ)的最大值的计算,解题时要注意根的判别式、韦达定理、中点坐标公式、向量知识的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知一个算法,其流程图如图所示,则输出结果是( )


| A、7 | B、9 | C、11 | D、13 |
在等比数列{an}中,已知a3+a6=9,a2a7=8,则a32+a62=( )
| A、9 | B、65 | C、72 | D、99 |
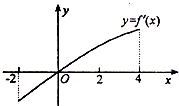 定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则
定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|