Question

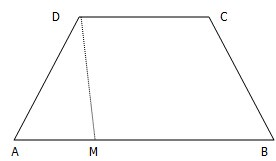如图所示的四边形ABCD为等腰梯形，两腰与底边的夹角为45°，上底边长为2，高为2．点M从A点出发，沿梯形的边AB，BC运动，最后到达点C，若x表示点M的移动路程，S表示线段DM在四边形ABCD内部扫过的面积．
（1）当S为梯形面积的一半时，求x的值；
（2）求S与x的函数关系式．

Answer 1

考点：根据实际问题选择函数类型

专题：应用题,函数的性质及应用

分析：（1）求出梯形的面积，即可求出S为梯形面积的一半时，x的值；
（2）分类讨论，即可求出S与x的函数关系式．

解答： 解：（1）∵四边形ABCD为等腰梯形，两腰与底边的夹角为45°，上底边长为2，高为2，
∴下底边长为6，
∴梯形面积为

(2+6)×2

2

=8，
∵S为梯形面积的一半，
∴

1

2

×AM×2=4，
∴AM=4，即x=4；
（2）当0＜x≤6时，S=

1

2

•x•2=x；
当6＜x≤6+2

2

时，S=8-

1

2

×2×（6+2

2

-x）=6+2

2

-x．

点评：本题考查根据实际问题选择函数类型，考查学生分析解决问题的能力，属于基础题．