题目内容
某市举办歌唱比赛,邀请了A、B、C、D四位资深音乐人担任评委,按照节目程序,每一位选手取得决赛资格后可通过抽签的方式选择一位评委作为导师,且他们对导师的选择是相互独立的,某组共有甲、乙、丙、丁四位选手取得了决赛资格,获得了选择导师的机会.
(Ⅰ)求甲、乙、丙三人都选择A为导师的概率;
(Ⅱ)求四位选手至少有一人选择B作为导师的概率;
(Ⅲ)设四位选手选择C为导师的人数ξ,求ξ的分布列和数学期望.
(Ⅰ)求甲、乙、丙三人都选择A为导师的概率;
(Ⅱ)求四位选手至少有一人选择B作为导师的概率;
(Ⅲ)设四位选手选择C为导师的人数ξ,求ξ的分布列和数学期望.
考点:离散型随机变量及其分布列,相互独立事件的概率乘法公式,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)依题意知,每位选手选择每位明星作为导数的概率是
,设“甲、乙、丙三人都选择A为导师”为事件A,由此能求出甲、乙、丙三人都选择A为导师的概率.
(Ⅱ)设“四位选手都不选择B作为导师”为事件B,由此能求出四位选手至少有一人选择B作为导师的概率.
(Ⅲ)依题意ξ~(4,
),由此能求出ξ的分布列和Eξ.
| 1 |
| 4 |
(Ⅱ)设“四位选手都不选择B作为导师”为事件B,由此能求出四位选手至少有一人选择B作为导师的概率.
(Ⅲ)依题意ξ~(4,
| 1 |
| 4 |
解答:
解:(Ⅰ)依题意知,每位选手选择每位明星作为导数的概率是
,
设“甲、乙、丙三人都选择A为导师”为事件A,
则P(A)=
×
×
=
,
∴甲、乙、丙三人都选择A为导师的概率为
.
(Ⅱ)设“四位选手都不选择B作为导师”为事件B,
则P(B)=
×
×
×
=
,
∴四位选手至少有一人选择B作为导师的概率是:
P(
)=1-P(B)=1-
=
.
(Ⅲ)依题意ξ~(4,
),
∴ξ的分布列为P(ξ=k)=
×(
)k×(
)4-k=
×
,
k=0,1,2,3,4,
∴Eξ=4×
=1.
| 1 |
| 4 |
设“甲、乙、丙三人都选择A为导师”为事件A,
则P(A)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 64 |
∴甲、乙、丙三人都选择A为导师的概率为
| 1 |
| 64 |
(Ⅱ)设“四位选手都不选择B作为导师”为事件B,
则P(B)=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 81 |
| 256 |
∴四位选手至少有一人选择B作为导师的概率是:
P(
. |
| B |
| 81 |
| 256 |
| 175 |
| 256 |
(Ⅲ)依题意ξ~(4,
| 1 |
| 4 |
∴ξ的分布列为P(ξ=k)=
| C | k 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| C | k 4 |
| 34-k |
| 256 |
k=0,1,2,3,4,
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
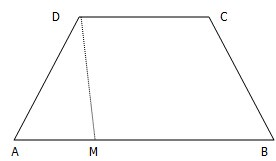 如图所示的四边形ABCD为等腰梯形,两腰与底边的夹角为45°,上底边长为2,高为2.点M从A点出发,沿梯形的边AB,BC运动,最后到达点C,若x表示点M的移动路程,S表示线段DM在四边形ABCD内部扫过的面积.
如图所示的四边形ABCD为等腰梯形,两腰与底边的夹角为45°,上底边长为2,高为2.点M从A点出发,沿梯形的边AB,BC运动,最后到达点C,若x表示点M的移动路程,S表示线段DM在四边形ABCD内部扫过的面积.