题目内容
已知二次函数f(x)=4x2+8x-3.
(1)指出函数y=f(x)图象的开口方向、对称轴方程、顶点坐标;
(2)求y=f(x)的最小值;
(3)写出函数y=f(x)的单调区间.
(4)当x∈[0,2]时,求函数y=f(x)的最大植和最小植.
(1)指出函数y=f(x)图象的开口方向、对称轴方程、顶点坐标;
(2)求y=f(x)的最小值;
(3)写出函数y=f(x)的单调区间.
(4)当x∈[0,2]时,求函数y=f(x)的最大植和最小植.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:首先把二次函数f(x)=4x2+8x-3的一般式转化为顶点式:y=4(x+1)2-7,然后根据顶点式进一步求得对称轴方程,顶点坐标,函数的最小值,单调区间,以及在某一定义域下的最大值和最小值.
解答:
解:二次函数f(x)=4x2+8x-3的一般式转化为顶点式:y=4(x+1)2-7,
(1)二次函数图象的开口方向向上,对称轴方程为:x=-1,顶点坐标为:(-1,-7);
(2)函数y=f(x)的最小值为:ymin=-7;
(3)函数y=f(x)的单调递增区间为:[-1,+∞);单调递减区间为(-∞,-1];
(4)二次函数f(x)=4x2+8x-3的开口方向向上,对称轴方程为:x=-1.
∴x∈[0,2]时,函数是单调递增函数.
∴当x=2时,函数y=f(x)的最大植为ymax=29.
∴当x=0时,函数y=f(x)的最小植为ymin=-3.
(1)二次函数图象的开口方向向上,对称轴方程为:x=-1,顶点坐标为:(-1,-7);
(2)函数y=f(x)的最小值为:ymin=-7;
(3)函数y=f(x)的单调递增区间为:[-1,+∞);单调递减区间为(-∞,-1];
(4)二次函数f(x)=4x2+8x-3的开口方向向上,对称轴方程为:x=-1.
∴x∈[0,2]时,函数是单调递增函数.
∴当x=2时,函数y=f(x)的最大植为ymax=29.
∴当x=0时,函数y=f(x)的最小植为ymin=-3.
点评:本题考查的知识点:二次函数一般式与顶点式的互化,对称轴方程,顶点坐标,函数的最小值,单调区间,以及在某一定义域下的最大值和最小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
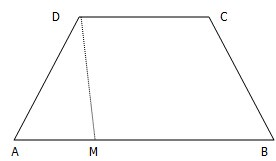 如图所示的四边形ABCD为等腰梯形,两腰与底边的夹角为45°,上底边长为2,高为2.点M从A点出发,沿梯形的边AB,BC运动,最后到达点C,若x表示点M的移动路程,S表示线段DM在四边形ABCD内部扫过的面积.
如图所示的四边形ABCD为等腰梯形,两腰与底边的夹角为45°,上底边长为2,高为2.点M从A点出发,沿梯形的边AB,BC运动,最后到达点C,若x表示点M的移动路程,S表示线段DM在四边形ABCD内部扫过的面积.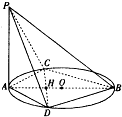 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.