题目内容
已知f(x)=sinx-
cosx(x∈[0,2π]),求单调递减区间.
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的求值,三角函数的图像与性质
分析:首先化简函数的解析式,然后结合三角函数的图象与性质即可进行求解.
解答:
解:∵f(x)=sinx-
cosx=2sin(x-
)
∵
+2kπ≤x-
≤
+2kπ,k∈Z,
∴2kπ+
≤x≤2kπ+
,(k∈Z),
∴f(x)的递减区间为[2kπ+
,2kπ+
],(k∈Z),
∵x∈[0,2π],
∴分f(x)的单调递减区间是[
,
].
| 3 |
| π |
| 3 |
∵
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
∴2kπ+
| 5π |
| 6 |
| 11π |
| 6 |
∴f(x)的递减区间为[2kπ+
| 5π |
| 6 |
| 11π |
| 6 |
∵x∈[0,2π],
∴分f(x)的单调递减区间是[
| 5π |
| 6 |
| 11π |
| 6 |
点评:本题主要考查了简单角的三角函数值的求解方法,两角和与差的正弦函数公式、三角函数的图象与性质等知识,考查了运算求解能力,属于中档题.

练习册系列答案
相关题目
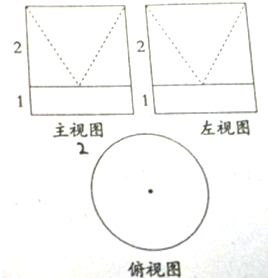 如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.
如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积. 如图,在三棱柱ABC-A1B1C1中,向量
如图,在三棱柱ABC-A1B1C1中,向量