题目内容
6.等差数列{an}的前n项和为Sn,且S3=6,a1=4,向量$\overrightarrow m$=(a5,3),$\overrightarrow n$=(1,a3),则向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于( )| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | -4 |
分析 先根据等差数列的求和公式以及投影的定义即可求出.
解答 解:∵S3=6=$\frac{3}{2}$(a1+a3),且 a3=a1+2d,a1=4,
∴d=-2,
∴a3=a1+2d=4+2×(-2)=0,a5=a1+4d=4+4×(-2)=-4,
∴向量$\overrightarrow m$=(-4,3),$\overrightarrow n$=(1,0),
∴$\overrightarrow{m}•\overrightarrow{n}$=-4,|$\overrightarrow{n}$|=1,
∴向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{n}|}$=-4,
故选:D.
点评 本题考查等差数列的求和公式以及向量投影的定义,属于中档题.

练习册系列答案
相关题目
14.(ax+$\frac{1}{x}$+y)6的展开式中,x2y2的系数为-480,则a=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
1.已知在平面直角坐标系xOy中圆C的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}+3cosθ\\ y=1+3sinθ.\end{array}$(θ为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+$\frac{π}{6}$)=0,则圆C截直线l所得弦长为( )
| A. | 6 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{35}$ |
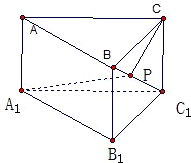 如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=3,BC=3,CC1=$\sqrt{3}$,P是BC1上一动点,则CP+PA1的最小值是$\sqrt{21}$.
如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=3,BC=3,CC1=$\sqrt{3}$,P是BC1上一动点,则CP+PA1的最小值是$\sqrt{21}$.