题目内容
14.(ax+$\frac{1}{x}$+y)6的展开式中,x2y2的系数为-480,则a=( )| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
分析 展开式中出现x2y2的项,是在6个因式(ax+$\frac{1}{x}$+y)6的乘积,其中有2个因式取y,有3个因式取ax,剩下的1个因式取$\frac{1}{x}$,据乘法原理求出a的值.
解答 解:(ax+$\frac{1}{x}$+y)6表示6个因式(ax+$\frac{1}{x}$+y)6的乘积,
其中有2个因式取y,有3个因式取ax,剩下的1个因式取$\frac{1}{x}$,即可得含x2y2的项,
故x2y2的系数为${C}_{6}^{2}$•${C}_{4}^{3}$•a3•${C}_{1}^{1}$=-480,∴a=-2,
故选:D.
点评 本题考查计数原理中的乘法原理,是常见的一种计数方法,属于中档题.

练习册系列答案
相关题目
5.直线x+y+1=0的倾斜角和斜率分别是( )
| A. | 45°,1 | B. | 135°,-1 | C. | 45°,-1 | D. | 90°,不存在 |
19.已知从球的一内接长方体的一个顶点出发的三条棱长分别为3,4,5,则此球的表面积为( )
| A. | 25π | B. | 50π | C. | 125π | D. | 均不正确 |
6.等差数列{an}的前n项和为Sn,且S3=6,a1=4,向量$\overrightarrow m$=(a5,3),$\overrightarrow n$=(1,a3),则向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | -4 |
4.若函数f(x)=2sin(ωx+φ)的图象(部分)如图所示,则ω和φ的可能取值是( )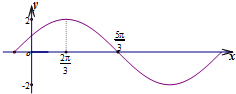

| A. | ω=1,φ=$\frac{π}{3}$ | B. | ω=1,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ |