题目内容
1.已知在平面直角坐标系xOy中圆C的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}+3cosθ\\ y=1+3sinθ.\end{array}$(θ为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+$\frac{π}{6}$)=0,则圆C截直线l所得弦长为( )| A. | 6 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{35}$ |
分析 求出圆C的圆心和半径,直线l的普通方程,计算圆心到直线l的距离,利用垂径定理求出弦长.
解答 解:圆C的普通方程为(x-$\sqrt{3}$)2+(y-1)2=9,
∴圆C的圆心为C($\sqrt{3}$,1),半径为r=3.
直线l的极坐标方程可化为$\frac{\sqrt{3}}{2}$ρcosθ-$\frac{1}{2}$ρsinθ=0,
∴直线l的普通方程为$\sqrt{3}$x-y=0,
∴C到直线l的距离d=$\frac{|3-1|}{2}$=1,
∴圆C截直线l所得弦长为2$\sqrt{{r}^{2}-{d}^{2}}$=4$\sqrt{2}$.
故选C.
点评 本题考查了直线与圆的位置关系,极坐标方程与普通方程的转化,属于中档题.

练习册系列答案
相关题目
6.等差数列{an}的前n项和为Sn,且S3=6,a1=4,向量$\overrightarrow m$=(a5,3),$\overrightarrow n$=(1,a3),则向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | -4 |
13.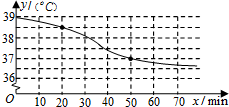 现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
 现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )| A. | 0.05(℃/min) | B. | -0.05(℃/min) | C. | 0.025(℃/min) | D. | -0.025(℃/min) |
11.函数f(x)=5cos(4x+$\frac{π}{4}$)的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
 如图,已知过点P(4,3)的光线,经x轴上一点A反射后的射线l过点Q(0,5).
如图,已知过点P(4,3)的光线,经x轴上一点A反射后的射线l过点Q(0,5).