题目内容
16.已知$\frac{π}{2}$<α<π,0<β<$\frac{π}{2}$,cosα=-$\frac{3}{5}$,sinβ=$\frac{5}{13}$,求sin(α+β)的值.分析 由已知利用同角三角函数基本关系式可求$sinα=\frac{4}{5}$,$cosβ=\frac{12}{13}$,进而利用两角和的正弦函数公式即可计算求值得解.
解答 解:∵$\frac{π}{2}$<α<π,0<β<$\frac{π}{2}$,cosα=-$\frac{3}{5}$,sinβ=$\frac{5}{13}$,
∴$sinα=\frac{4}{5}$,$cosβ=\frac{12}{13}$┅┅┅(6分)
∴sin(α+β)=sinαcosβ+cosαsinβ=$\frac{4}{5}×\frac{12}{13}$+(-$\frac{3}{5}$)×$\frac{5}{13}$=$\frac{33}{65}$.┅┅┅(12分)
点评 本题主要考查了同角三角函数基本关系式,两角和的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
6.等差数列{an}的前n项和为Sn,且S3=6,a1=4,向量$\overrightarrow m$=(a5,3),$\overrightarrow n$=(1,a3),则向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | -4 |
7.已知f(x+2)=2x,则f(2)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
4.若函数f(x)=2sin(ωx+φ)的图象(部分)如图所示,则ω和φ的可能取值是( )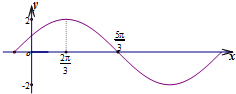

| A. | ω=1,φ=$\frac{π}{3}$ | B. | ω=1,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ |
11.函数f(x)=5cos(4x+$\frac{π}{4}$)的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
8.已知中心在原点,焦点F1、F2在x轴上的双曲线经过点P(4,2),△PF1F2的内切圆与x轴相切于点Q(2$\sqrt{2}$,0),则双曲线的实轴长为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |