在三角形ABC中.若sinB=2sinAcosC.那么三角形ABC一定是等腰三角形．题目和参考答案——青夏教育精英家教网—

题目内容

16．在三角形ABC中，若sinB=2sinAcosC，那么三角形ABC一定是等腰三角形．

分析 sinB=sin（A+C）=2sinAcosC，展开化简即可得出．

解答解：∵sinB=sin（A+C）=2sinAcosC，
∴sin（A-C）=0，A，C∈（0，π），∴A=C，
因此三角形ABC一定是等腰三角形．
故答案为：等腰．

点评本题考查了和差公式、诱导公式、三角形内角和定理，考查了推理能力与计算能力，属于中档题．

练习册系列答案

快乐假期暑假作业新疆人民出版社系列答案

相关题目

6．如图，ABCD-A₁B₁C₁D₁为正方体，则下列结论错误的是（　　）

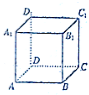
	A．	A₁C⊥B₁D₁		B．	B₁D₁∥平面BDC₁
	C．	A₁C⊥平面BDC₁		D．	异面直线AD与BC₁所成的角为30°

7．已知向量$\overrightarrow{a}$=（3，$\sqrt{3}$），$\overrightarrow{b}$=（-$\sqrt{3}$，1），则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角大小是$\frac{2π}{3}$．

4．已知P和不共线三点A，B，C四点共面且对于空间任一点O，都有$\overrightarrow{OP}$=2$\overrightarrow{OA}$+$\overrightarrow{OB}$+λ$\overrightarrow{OC}$，则λ=2．

11．（1+x）⁷（1-x）⁵的展开式中，含x⁶项的系数是0．

1．已知函数f（x）=log_a（-x²+log_2ax）对任意x∈（0，$\frac{1}{2}$）都有意义，则实数a的取值范围是（　　）

A．

[$\frac{1}{128}$，$\frac{1}{2}$）

B．

[$\frac{1}{64}$，$\frac{1}{2}$）

C．

[$\frac{1}{32}$，$\frac{1}{2}$）

D．

[$\frac{1}{16}$，$\frac{1}{2}$）

8．若函数y=（$\frac{2}{2c+1}$）^-x在R上单调递减，且函数g（x）=lg（2cx²+2x+1）的值域为R，则c的取值范围是0≤c＜$\frac{1}{2}$．

5．直线x+y+1=0的倾斜角和斜率分别是（　　）

6．等差数列{a_n}的前n项和为S_n，且S₃=6，a₁=4，向量$\overrightarrow m$=（a₅，3），$\overrightarrow n$=（1，a₃），则向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于（　　）

试题分类