题目内容
17.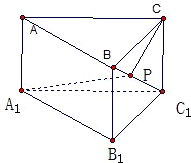 如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=3,BC=3,CC1=$\sqrt{3}$,P是BC1上一动点,则CP+PA1的最小值是$\sqrt{21}$.
如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=3,BC=3,CC1=$\sqrt{3}$,P是BC1上一动点,则CP+PA1的最小值是$\sqrt{21}$.
分析 本题考查图形的展开,直线距离最小;连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,连A1C,则A1C的长度就是所求的最小值.
解答 解:连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,如图所示,连A1C,则A1C的长度就是所求的最小值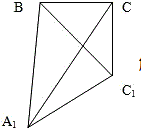
A1C1=3,CC1=$\sqrt{3}$,BC=3,A1B=$\sqrt{21}$,△CBC1是直角三角形,根据边长关系可知∠CC1B=60°
△A1BC1根据边长关系可知∠A1C1B=90°
∴∠A1C1C=150°
利用余弦定理:$C{{C}_{1}}^{2}+{A}_{1}{{C}_{1}}^{2}-2$A1C1•CC1•cos50°=${A}_{1}{C}^{2}$
∴A1C=$\sqrt{21}$
故答案为$\sqrt{21}$.
点评 本题考查棱柱的结构特征,图形的展开,直线距离最小;连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,连A1C,则A1C的长度就是所求的最小值,同时利用到利用余弦定理.空间问题有时候是可以转化成平面问题来解决的.属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.直线x+y+1=0的倾斜角和斜率分别是( )
| A. | 45°,1 | B. | 135°,-1 | C. | 45°,-1 | D. | 90°,不存在 |
6.等差数列{an}的前n项和为Sn,且S3=6,a1=4,向量$\overrightarrow m$=(a5,3),$\overrightarrow n$=(1,a3),则向量$\overrightarrow m$在$\overrightarrow n$方向上的投影等于( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | -4 |
7.已知f(x+2)=2x,则f(2)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |