题目内容
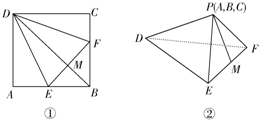如图，在正方形ABCD中，E，F分别是AB，BC的中点，现在沿DE，DF及EF把△ADE，△CDF和△BEF折起，使A，B，C三点重合，重合后的点记作P，那么在四面体P-DEF中必有（ ）| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |
考点：直线与平面垂直的判定,棱锥的结构特征
专题：空间位置关系与距离
分析：根据条件，利用线面垂直和面面垂直的判定定理进行判断．
解答：
解：因为E，F分别是AB、BC的中点，所以BD⊥EF，
因为DA⊥AE，DC⊥CF，所以折叠后DP⊥PE，DP⊥PF，
因为PE∩PF=P，
所以DP⊥面PEF，
故选：A．
因为DA⊥AE，DC⊥CF，所以折叠后DP⊥PE，DP⊥PF，
因为PE∩PF=P，
所以DP⊥面PEF，
故选：A．
点评：本题主要考查了线面垂直和面面垂直的判定，要求熟练掌握相应的判定定理．
练习册系列答案
全能测控期末小状元系列答案
相关题目
函数f（x）=2x+2x-3的零点所在的大致区间是（ ）
A、（0，
| ||
B、（
| ||
| C、（1，2） | ||
| D、（2，3） |
在极坐标方程中，曲线C的方程是ρ=4sinθ，过点（4，
）作曲线C的切线，切线长为（ ）
| π |
| 6 |
| A、4 | ||
| B、7 | ||
C、2
| ||
| D、3 2 |