题目内容
命题“存在x∈R，使得
+
=0”的否定是 ．
| x2+1 |
| 1-x2 |
考点：命题的否定
专题：简易逻辑
分析：直接利用特称命题的否定是全称命题写出结果即可．
解答：
解：因为特称命题的否定是全称命题，所以，命题“存在x∈R，使得
+
=0”的否定是：对任意x∈R，都有
+
≠0．
故答案为：对任意x∈R，都有
+
≠0．
| x2+1 |
| 1-x2 |
| x2-1 |
| 1-x2 |
故答案为：对任意x∈R，都有
| x2-1 |
| 1-x2 |
点评：本题考查命题的复数特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知
=1-bi，其中a，b是实数，i是虚数单位，则|a-bi|=（ ）
| a |
| 1+i |
| A、3 | ||
| B、2 | ||
| C、5 | ||
D、
|
已知复数z=
，则z在复平面内对应的点位于（ ）
| 1 |
| i(i+1) |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
复数z=
在复平面内对应的点的坐标为（ ）
| 1 |
| i |
| A、（0，-1） |
| B、（0，1） |
| C、（-1，0） |
| D、（1，0） |
在不等式组
，所表示的平面区域内所有的整点（横、纵坐标均为整数的点对称为整点）中任取3个点，则这3个点恰能成为一个三角形的三个顶点的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
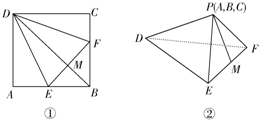如图，在正方形ABCD中，E，F分别是AB，BC的中点，现在沿DE，DF及EF把△ADE，△CDF和△BEF折起，使A，B，C三点重合，重合后的点记作P，那么在四面体P-DEF中必有（ ）| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |