题目内容
已知双曲线
-
=1的一条渐近线为y=
x,右焦点F到x=
的距离为
,求双曲线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| a2 |
| c |
| 3 |
| 2 |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线
-
=1的一条渐近线为y=
x,右焦点F到x=
的距离为
,可得
,求出a,b,即可求双曲线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| a2 |
| c |
| 3 |
| 2 |
|
解答:
解:由题意,
,
∴a=2,c=4,b=2
,
∴双曲线的方程为
-
=1.
|
∴a=2,c=4,b=2
| 3 |
∴双曲线的方程为
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题考查双曲线的标准方程的求法,考查双曲线的性质,正确计算是关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在不等式组
,所表示的平面区域内所有的整点(横、纵坐标均为整数的点对称为整点)中任取3个点,则这3个点恰能成为一个三角形的三个顶点的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
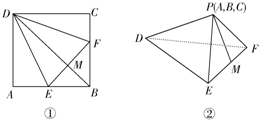 如图,在正方形ABCD中,E,F分别是AB,BC的中点,现在沿DE,DF及EF把△ADE,△CDF和△BEF折起,使A,B,C三点重合,重合后的点记作P,那么在四面体P-DEF中必有( )
如图,在正方形ABCD中,E,F分别是AB,BC的中点,现在沿DE,DF及EF把△ADE,△CDF和△BEF折起,使A,B,C三点重合,重合后的点记作P,那么在四面体P-DEF中必有( )| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |
设f(x)=ax3+bx2+cx+d(a≠0).已知五个方程的相异实根个数如下表所述﹕
α为关于f(x)的极大值﹐下列选项中正确的是( )
| f(x)-20=0 | 1 | f(x)+10=0 | 1 |
| f(x)-10=0 | 3 | f(x)+20=0 | 1 |
| f(x)=0 | 3 |
| A、0<α<10 |
| B、10<α<20 |
| C、-10<α<0 |
| D、-20<α<-10 |
