题目内容
在极坐标方程中，曲线C的方程是ρ=4sinθ，过点（4，
）作曲线C的切线，切线长为（ ）
| π |
| 6 |
| A、4 | ||
| B、7 | ||
C、2
| ||
| D、3 2 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：由曲线C的方程ρ=4sinθ，可得ρ2=4ρsinθ，化为x2+（y-2）2=4．圆心C（0，2），r=2．点（4，
）化为直角坐标P(2
，2)．利用切线长=
即可得出．
| π |
| 6 |
| 3 |
| CP2-r2 |
解答：
解：由曲线C的方程ρ=4sinθ，可得ρ2=4ρsinθ，
∴x2+y2=4y，配方为x2+（y-2）2=4．圆心C（0，2），r=2．
点（4，
）化为直角坐标P(4cos
，4sin
)，即P(2
，2)．
CP=2
．
切线长=
=
=2
．
故选：C．
∴x2+y2=4y，配方为x2+（y-2）2=4．圆心C（0，2），r=2．
点（4，
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
CP=2
| 3 |
切线长=
| CP2-r2 |
(2
|
| 2 |
故选：C．
点评：本题考查了极坐标方程化为直角坐标方程、圆的标准方程、切线性质及其长度，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
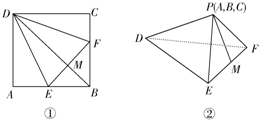如图，在正方形ABCD中，E，F分别是AB，BC的中点，现在沿DE，DF及EF把△ADE，△CDF和△BEF折起，使A，B，C三点重合，重合后的点记作P，那么在四面体P-DEF中必有（ ）| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |
设f（x）=ax3+bx2+cx+d（a≠0）．已知五个方程的相异实根个数如下表所述﹕
α为关于f（x）的极大值﹐下列选项中正确的是（ ）
| f（x）-20=0 | 1 | f（x）+10=0 | 1 |
| f（x）-10=0 | 3 | f（x）+20=0 | 1 |
| f（x）=0 | 3 |
| A、0＜α＜10 |
| B、10＜α＜20 |
| C、-10＜α＜0 |
| D、-20＜α＜-10 |
函数y=ecosx（-π≤x≤π）的大致图象为（ ）
A、 |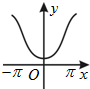
B、 |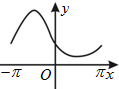
C、 |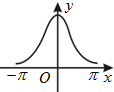
D、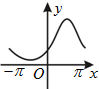 |