题目内容
O是平面上一定点，A、B、C是平面上不共线三点，动点P满足
=
+λ(
+
)，λ∈R，则P点的轨迹为 ．
| OP |
| OA |
| ||
|
|
| ||
|
|
考点：轨迹方程,向量数乘的运算及其几何意义
专题：综合题,平面向量及应用
分析：先根据
、
分别表示向量
、
方向上的单位向量，确定
+
的方向与∠BAC的角平分线一致，再由
=
+λ(
+
)，可得到
-
=
=λ（
+
），可得答案．
| ||
|
|
| ||
|
|
| AB |
| AC |
| ||
|
|
| ||
|
|
| OP |
| OA |
| ||
|
|
| ||
|
|
| OP |
. |
| OA |
| AP |
| ||
|
|
| ||
|
|
解答：
解：∵
、
分别表示向量
、
方向上的单位向量
∴
+
的方向与∠BAC的角平分线一致
又∵
=
+λ(
+
)，
∴
-
=
=λ（
+
）
∴向量
的方向与∠BAC的角平分线一致
∴P点的轨迹为∠BAC的角平分线所在直线．
故答案为：∠BAC的角平分线所在直线．
| ||
|
|
| ||
|
|
| AB |
| AC |
∴
| ||
|
|
| ||
|
|
又∵
| OP |
| OA |
| ||
|
|
| ||
|
|
∴
| OP |
. |
| OA |
| AP |
| ||
|
|
| ||
|
|
∴向量
| AP |
∴P点的轨迹为∠BAC的角平分线所在直线．
故答案为：∠BAC的角平分线所在直线．
点评：本题主要考查向量的线性运算和几何意义．属基础题．
练习册系列答案
相关题目
复数z=
在复平面内对应的点的坐标为（ ）
| 1 |
| i |
| A、（0，-1） |
| B、（0，1） |
| C、（-1，0） |
| D、（1，0） |
如图，为测量坡高MN，选择A和另一个山坡的坡顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°．已知坡高BC=50米，则坡高MN=
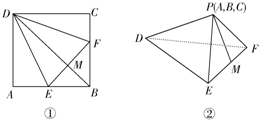如图，在正方形ABCD中，E，F分别是AB，BC的中点，现在沿DE，DF及EF把△ADE，△CDF和△BEF折起，使A，B，C三点重合，重合后的点记作P，那么在四面体P-DEF中必有（ ）| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |
