题目内容
已知函数f（x）=3sin（2x+
），x∈R．
（1）求f（
）的值；
（2）若sinθ=
，θ∈（0，
），求f（
-θ）．
| π |
| 6 |
（1）求f（
| π |
| 12 |
（2）若sinθ=
| 4 |
| 5 |
| π |
| 2 |
| 5π |
| 12 |
考点：正弦函数的图象
专题：三角函数的求值
分析：（1）由条件直接计算f（
）的值．
（2）由条件利用同角三角函数的基本关系求得cosθ的值，再根据f（
-θ）=6sinθcosθ，求得结果．
| π |
| 12 |
（2）由条件利用同角三角函数的基本关系求得cosθ的值，再根据f（
| 5π |
| 12 |
解答：
解：（1）由函数f（x）=3sin（2x+
），x∈R，可得f（
）=3sin
=
．
（2）由sinθ=
，θ∈（0，
），可得cosθ=
=
，
∴f（
-θ）=3sin（
-2θ+
）=3sin2θ=6sinθcosθ=6•
•
=
．
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
3
| ||
| 2 |
（2）由sinθ=
| 4 |
| 5 |
| π |
| 2 |
| 1-sin2θ |
| 3 |
| 5 |
∴f（
| 5π |
| 12 |
| 5π |
| 6 |
| π |
| 6 |
| 4 |
| 5 |
| 3 |
| 5 |
| 72 |
| 25 |
点评：本题主要考查同角三角函数的基本关系、诱导公式的应用，属于基础题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
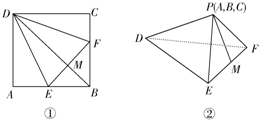如图，在正方形ABCD中，E，F分别是AB，BC的中点，现在沿DE，DF及EF把△ADE，△CDF和△BEF折起，使A，B，C三点重合，重合后的点记作P，那么在四面体P-DEF中必有（ ）| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |