题目内容
椭圆C的两焦点坐标分别为F1(-5
,0)和F2(5
,0),且椭圆经过点P(-5
,-
).
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q(-6,0)作直线l交椭圆C于M、N两点(直线l不与x轴重合),A为椭圆的左顶点,试证明:∠MAN=90°.
| 3 |
| 3 |
| 3 |
| 5 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q(-6,0)作直线l交椭圆C于M、N两点(直线l不与x轴重合),A为椭圆的左顶点,试证明:∠MAN=90°.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)椭圆方程为
+
=1(a>b>0),由已知得c2=a2-b2=75,
+
•
=1,由此能求出椭圆方程.
(Ⅱ)设直线MN的方程为:x=my-6由
得:(m2+4)y2-12my-64=0,由此能证明∠MAN的大小必为定值
.
| x2 |
| a2 |
| y2 |
| b2 |
| 75 |
| a2 |
| 1 |
| b2 |
| 25 |
| 4 |
(Ⅱ)设直线MN的方程为:x=my-6由
|
| π |
| 2 |
解答:
(Ⅰ)解:由题意,设椭圆方程为
+
=1(a>b>0),
由已知则有c2=a2-b2=75,
+
•
=1,
联立解得a2=100,b2=25,
故所求椭圆方程为
+
=1…..(4分)
(Ⅱ)证明:设直线MN的方程为:x=my-6
由
得:(m2+4)y2-12my-64=0,
因为点(-6,0)在椭圆内部,
直线必与椭圆相交于两点,即△>0恒成立
设M(x1,y1),N(x2,y2),
则y1+y2=
,y1•y2=
,…..(8分)
则
•
=(x1+10,y1)•(x2+10,y2)
=(my1+4,y1)•(my2+4,y2)
=(m2+1)y1y2+4m(y1+y2)+16
将y1+y2=
,y1•y2=
,
代入上式整理,得
•
=0,∴∠MAN=
,
则∠MAN的大小必为定值
….(12分)
| x2 |
| a2 |
| y2 |
| b2 |
由已知则有c2=a2-b2=75,
| 75 |
| a2 |
| 1 |
| b2 |
| 25 |
| 4 |
联立解得a2=100,b2=25,
故所求椭圆方程为
| x2 |
| 100 |
| y2 |
| 25 |
(Ⅱ)证明:设直线MN的方程为:x=my-6
由
|
因为点(-6,0)在椭圆内部,
直线必与椭圆相交于两点,即△>0恒成立
设M(x1,y1),N(x2,y2),
则y1+y2=
| 12m |
| m2+4 |
| -64 |
| m2+4 |
则
| AM |
| AN |
=(my1+4,y1)•(my2+4,y2)
=(m2+1)y1y2+4m(y1+y2)+16
将y1+y2=
| 12m |
| m2+4 |
| -64 |
| m2+4 |
代入上式整理,得
| AM |
| AN |
| π |
| 2 |
则∠MAN的大小必为定值
| π |
| 2 |
点评:本题考查椭圆方程的求法,考查角为定值的证明,解题时要认真审题,注意韦达定理的合理运用.

练习册系列答案
相关题目
对任意的锐角α,β下列不等关系中正确的是( )
| A、sin(α+β)>sinα+sinβ |
| B、sin(α+β)>cosα+cosβ |
| C、cos(α+β)<cosα+sinβ |
| D、cos(α+β)>sinα+sinβ |


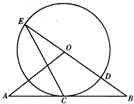 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于点E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于点E、D.