题目内容
已知tanα=-3,且α是第二象限的角,
(1)求sinα,cosα的值;
(2)求sin(2α-
)的值.
(1)求sinα,cosα的值;
(2)求sin(2α-
| π |
| 6 |
考点:两角和与差的正弦函数,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)由sinα=-3cosα和sin2α+cos2α=1结合角的范围,解方程组可得;(2)由(1)可得sin2α和cos2α,代入两角差的正弦公式计算可得.
解答:
解:(1)∵tanα=-3,∴sinα=-3cosα,
又sin2α+cos2α=1,
解得
,或
∵α是第二象限的角,∴
(2)由(1)可得sin2α=2sinαcosα=-
,
cos2α=cos2α-sin2α=-
,
∴sin(2α-
)=
sin2α-
cos2α
=
×(-
)-
×(-
)=
.
又sin2α+cos2α=1,
解得
|
|
∵α是第二象限的角,∴
|
(2)由(1)可得sin2α=2sinαcosα=-
| 3 |
| 5 |
cos2α=cos2α-sin2α=-
| 4 |
| 5 |
∴sin(2α-
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
4-3
| ||
| 10 |
点评:本题考查两角和与差的正弦函数,涉及同角三角函数的基本关系,属基础题.

练习册系列答案
相关题目
正方体ABCD-A1B1C1D1中,二面角A-BD1-B1的大小为( )
| A、90° | B、60° |
| C、120° | D、45° |
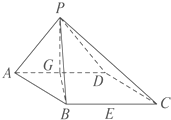 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.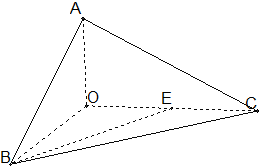 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.