题目内容
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.

(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求BP的长;
(Ⅲ)求直线AP与平面BCD所成的角.

(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求BP的长;
(Ⅲ)求直线AP与平面BCD所成的角.
考点:直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(I)由已知中面ABC⊥面BCQ,及=∠BCD=90°,我们根据面面垂直的性质定理,我们易得CQ⊥面ABC,进而根据线面垂直的定义,即可得到AB⊥CQ;
(Ⅱ)作AO⊥BC,垂足为O,则AO⊥平面BCQ,连接OP,利用AP=DP,即可求BP的长;
(Ⅲ)由(I)知AO⊥平面BCD,可得∠APO是直线AP与平面BCD所成的角.
(Ⅱ)作AO⊥BC,垂足为O,则AO⊥平面BCQ,连接OP,利用AP=DP,即可求BP的长;
(Ⅲ)由(I)知AO⊥平面BCD,可得∠APO是直线AP与平面BCD所成的角.
解答:
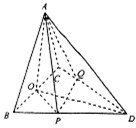 (I)证明:∵面ABC⊥面BCQ
(I)证明:∵面ABC⊥面BCQ
又CQ⊥BC
∴CQ⊥面ABC
∴CQ⊥AB;
(Ⅱ)解:作AO⊥BC,垂足为O,则AO⊥平面BCQ,连接OP,
设AB=4,则BD=2,设BP=x,
由题意AP=DP,∴(
)2+x2-2×
×xcos45°+(
)2=(2-x)2,
∴x=1;
(Ⅲ)解:由(I)知AO⊥平面BCD,
∴∠APO是直线AP与平面BCD所成的角,
∴∠APO=45°,
∴直线AP与平面BCD所成的角为45°.
 (I)证明:∵面ABC⊥面BCQ
(I)证明:∵面ABC⊥面BCQ又CQ⊥BC
∴CQ⊥面ABC
∴CQ⊥AB;
(Ⅱ)解:作AO⊥BC,垂足为O,则AO⊥平面BCQ,连接OP,
设AB=4,则BD=2,设BP=x,
由题意AP=DP,∴(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴x=1;
(Ⅲ)解:由(I)知AO⊥平面BCD,
∴∠APO是直线AP与平面BCD所成的角,
∴∠APO=45°,
∴直线AP与平面BCD所成的角为45°.
点评:本题考查的知识点是直线与平面垂直的性质,直线与平面所成的角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列函数中在R上是增函数的是( )
| A、y=lnx |
| B、y=tanx |
| C、y=ex |
| D、y=|x| |
下列函数是偶函数,且在(0,+∞)上单调递增的是( )
| A、y=x3 | ||
B、y=(
| ||
| C、y=1-x2 | ||
| D、y=lgx2 |
“a≤8”是“关于实数x的不等式|x-5|+|x+3|>a对任意x∈R恒成立”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=(1-sinθ,1),
=(
,1+sinθ),若
∥
,则锐角θ等于( )
| a |
| b |
| 1 |
| 4 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、75° |