题目内容
已知四棱锥P-ABCD中,底面ABCD为等腰梯形,PD⊥平面ABCD,AB=2CD,PD=AD=CD=1.
(1)求AD与PB所成角的大小;
(2)求AB与面PBD所成角的大小;
(3)求面PAD与面PBC所成锐二面角的正切值.
(1)求AD与PB所成角的大小;
(2)求AB与面PBD所成角的大小;
(3)求面PAD与面PBC所成锐二面角的正切值.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间角
分析:(1)以D为原点,以DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出AD与PB所成角.
(2)求出平面PBD的法向量,由此能求出AB与面PBD所成角的大小.
(3)求出面PAD的法向量和面PBC的法向量,利用向量法能求出面PAD与面PBC所成锐二面角的正切值.
(2)求出平面PBD的法向量,由此能求出AB与面PBD所成角的大小.
(3)求出面PAD的法向量和面PBC的法向量,利用向量法能求出面PAD与面PBC所成锐二面角的正切值.
解答:
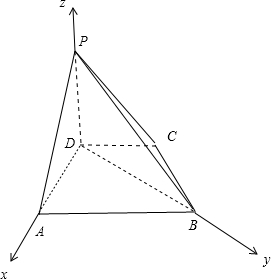 解:(1)四棱锥P-ABCD中,底面ABCD为等腰梯形,
解:(1)四棱锥P-ABCD中,底面ABCD为等腰梯形,
PD⊥平面ABCD,AB=2CD,PD=AD=CD=1,
∴DA、DB、DP两两垂直,
以D为原点,以DA为x轴,DB为y轴,DP为z轴,
建立空间直角坐标系,
A(1,0,0),D(0,0,0),P(0,0,1),
B(0,
,0),C(-
,
,0)
=(1,0,0),
=(0,
,-1),
设AD与PB所成角为θ,
cosθ=|<
,
>|=|
|=0,
∴AD与PB所成角为90°.
(2)∵平面PBD的法向量
=(1,0,0),
=(1,-
,0),
设AB与面PBD所成角为α,
则sinα=|cos<
,
>|=|
|=
,
∴α=30°,
∴AB与面PBD所成角为30°.
(3)面PAD的法向量
=(0,1,0),
=(-
,
,-1),
=(0,
,-1),
设面PBC的法向量
=(x,y,z),
则
,
取y=
,得
=(-3,
,3),
设面PAD与面PBC所成锐二面角的平面角为β,
cosβ=|cos<
,
>|=|
|=
.
sinβ=
=
,
∴tanβ=
.
∴面PAD与面PBC所成锐二面角的正切值是
.
 解:(1)四棱锥P-ABCD中,底面ABCD为等腰梯形,
解:(1)四棱锥P-ABCD中,底面ABCD为等腰梯形,PD⊥平面ABCD,AB=2CD,PD=AD=CD=1,
∴DA、DB、DP两两垂直,
以D为原点,以DA为x轴,DB为y轴,DP为z轴,
建立空间直角坐标系,
A(1,0,0),D(0,0,0),P(0,0,1),
B(0,
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| DA |
| PB |
| 3 |
设AD与PB所成角为θ,
cosθ=|<
| DA |
| PB |
| 0 |
| 2 |
∴AD与PB所成角为90°.
(2)∵平面PBD的法向量
| n |
| BA |
| 3 |
设AB与面PBD所成角为α,
则sinα=|cos<
| BA |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
∴α=30°,
∴AB与面PBD所成角为30°.
(3)面PAD的法向量
| m |
| PC |
| 1 |
| 2 |
| ||
| 2 |
| PB |
| 3 |
设面PBC的法向量
| p |
则
|
取y=
| 3 |
| p |
| 3 |
设面PAD与面PBC所成锐二面角的平面角为β,
cosβ=|cos<
| m |
| p |
| ||
|
| ||
| 7 |
sinβ=
1-
|
| ||
| 7 |
∴tanβ=
| 6 |
∴面PAD与面PBC所成锐二面角的正切值是
| 6 |
点评:本题考查异面直线所成角的求法,考查直线与平面所成角的大小的求法,考查二面角的正切值的求法,解题时要注意向量法的合理运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
“a≤8”是“关于实数x的不等式|x-5|+|x+3|>a对任意x∈R恒成立”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
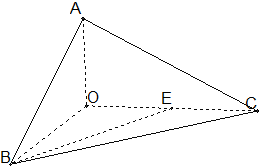 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为
有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为