题目内容
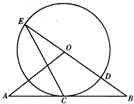 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于点E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于点E、D.(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED=
| 1 |
| 2 |
考点:弦切角,圆的切线的判定定理的证明
专题:立体几何
分析:(I)利用等腰三角形的性质和切线的定义即可证明;
(II)利用圆的性质可得
=
.再利用切线的性质可得△CBD∽△EBC,于是
=
=
.设BD=x,BC=2x,利用切割线定理可得BC2=BD•BE,代入解出即可.
(II)利用圆的性质可得
| CD |
| EC |
| 1 |
| 2 |
| BD |
| BC |
| CD |
| EC |
| 1 |
| 2 |
解答:
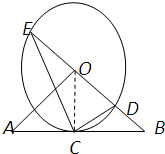 (Ⅰ)证明:如图,连接OC,
(Ⅰ)证明:如图,连接OC,
∵OA=OB,CA=CB,∴OC⊥AB,∴AB是⊙O的切线.
(Ⅱ)∵ED是直径,∴∠ECD=90°,
在Rt△BCD中,∵tan∠CED=
,∴
=
.
∵AB是⊙O的切线,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△CBD∽△EBC,∴
=
=
.
设BD=x,BC=2x,
又BC2=BD•BE,∴(2x)2=x•(x+12).
解得:x1=0,x2=4,
∵BD=x>0,∴BD=4.
∴OA=OB=BD+OD=4+6=10.
 (Ⅰ)证明:如图,连接OC,
(Ⅰ)证明:如图,连接OC,∵OA=OB,CA=CB,∴OC⊥AB,∴AB是⊙O的切线.
(Ⅱ)∵ED是直径,∴∠ECD=90°,
在Rt△BCD中,∵tan∠CED=
| 1 |
| 2 |
| CD |
| EC |
| 1 |
| 2 |
∵AB是⊙O的切线,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△CBD∽△EBC,∴
| BD |
| BC |
| CD |
| EC |
| 1 |
| 2 |
设BD=x,BC=2x,
又BC2=BD•BE,∴(2x)2=x•(x+12).
解得:x1=0,x2=4,
∵BD=x>0,∴BD=4.
∴OA=OB=BD+OD=4+6=10.
点评:本题考查了等腰三角形的性质、切线的定义、圆的性质、相似三角形的性质、切割线定理等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
能正确表示图中阴影部分的选项为( )


| A、∁U(M∪N) |
| B、∁U(M∩N) |
| C、(M∪N)∩∁U(M∩N) |
| D、(M∩N)∪∁U(M∪N) |
已知向量
=(1-sinθ,1),
=(
,1+sinθ),若
∥
,则锐角θ等于( )
| a |
| b |
| 1 |
| 4 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、75° |
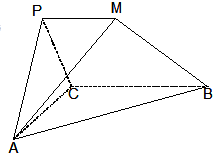 在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=2PM=4,AB=2
在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=2PM=4,AB=2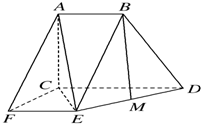 在直角梯形CDEF中,DC⊥CF,DC∥EF,CD=CF=2EF=2.将它绕CD旋转得到CDBA,使得平面CDBA⊥平面CDEF.
在直角梯形CDEF中,DC⊥CF,DC∥EF,CD=CF=2EF=2.将它绕CD旋转得到CDBA,使得平面CDBA⊥平面CDEF.