题目内容
（1）如图①、②、③、④为四个平面图，数一数，每个平面图各有多少个顶点？多少条边？它们把平面分成了多少个区域？请将结果填入下表中：
（2）观察上表，推断一个平面图形的顶点数V，边数E，区域数F之间有什么关系；
（3）现已知某个平面图形有999个顶点，且围成了999个区域，试根据以上关系确定这个平面图形的边数．
| 顶点 | 边数 | 区域数 | |
| ① | |||
| ② | |||
| ③ | |||
| ④ |
（3）现已知某个平面图形有999个顶点，且围成了999个区域，试根据以上关系确定这个平面图形的边数．
考点：进行简单的合情推理
专题：推理和证明
分析：（1）由所给的b图表格数据得出：
①图顶点数为3个，3条边，围成1个区域；
②图有8个顶点，12条边，围成5个区域；
③图有6个顶点，9条边，围成4个区域；
④图有10个顶点，15条边，围成6个区域；
（2）根据表中数值得出平面图形的顶点数、边数、区域数之间的关系为：顶点数+区域数-1=边数；
（3）将数据代入（2）的公式计算即可．
①图顶点数为3个，3条边，围成1个区域；
②图有8个顶点，12条边，围成5个区域；
③图有6个顶点，9条边，围成4个区域；
④图有10个顶点，15条边，围成6个区域；
（2）根据表中数值得出平面图形的顶点数、边数、区域数之间的关系为：顶点数+区域数-1=边数；
（3）将数据代入（2）的公式计算即可．
解答：
解：（1）
（2）根据表中数值，可得顶点数V，边数E，区域数F的一种关系为：
顶点数+区域数-1=边数；
即V+F=E+1，
（3）由（2）得
E=V+F-1=1997
| 顶点 | 边数 | 区域数 | |
| ① | 3 | 3 | 1 |
| ② | 8 | 12 | 5 |
| ③ | 6 | 9 | 4 |
| ④ | 10 | 15 | 6 |
顶点数+区域数-1=边数；
即V+F=E+1，
（3）由（2）得
E=V+F-1=1997
点评：此题主要考查了计数方法的应用，根据四个不同的图形分别列举得出规律是解题的关键．
练习册系列答案
一课一练课时达标系列答案
相关题目
给出如图所示的算法框图，其功能是（ ）
| A、求a-b的值 |
| B、求b-a的值 |
| C、求|a-b|的值 |
| D、以上都不对 |
“a≤8”是“关于实数x的不等式|x-5|+|x+3|＞a对任意x∈R恒成立”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
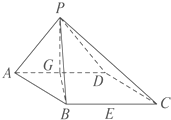如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，且∠DAB=60°．侧面PAD为正三角形，其所在的平面垂直于底面ABCD，G为AD边的中点．
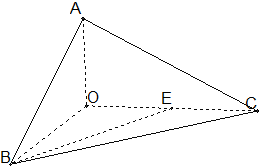如图，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．
有一海湾，海岸线近似为椭圆的一段弧NM，M、N为椭圆弧上两点，且MA⊥AB，NB⊥AB，AB间的距离为2公里，椭圆焦点为A、B，椭圆的短半轴长为