题目内容
设A、B、P是双曲线
-
=1(a>0,b>0)上不同的三个点,且A、B连线经过坐标原点,若直线PA、PB的斜率之积为
,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由于A,B连线经过坐标原点,所以A,B一定关于原点对称,利用直线PA,PB的斜率乘积,可寻求几何量之间的关系,从而可求离心率.
解答:
解:根据双曲线的对称性可知A,B关于原点对称,
设A(x1,y1),B(-x1,-y1),P(x,y),
则
-
=1,
-
=1
∴kPA•kPB=
•
=
=
,
∴该双曲线的离心率e=
=
.
故选:A.
设A(x1,y1),B(-x1,-y1),P(x,y),
则
| x12 |
| a2 |
| y12 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴kPA•kPB=
| y1-y |
| x1-x |
| -y1-y |
| -x1-x |
| b2 |
| a2 |
| 1 |
| 4 |
∴该双曲线的离心率e=
1+
|
| ||
| 2 |
故选:A.
点评:本题主要考查双曲线的几何性质,考查点差法,关键是设点代入化简,应注意双曲线几何量之间的关系.

练习册系列答案
相关题目
以正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC,则双曲线的离心率为( )
A、
| ||
| B、2 | ||
C、
| ||
D、2
|
判断下列命题的真假,其中为真命题的是( )
| A、?x∈R,x2+1=0 |
| B、?x∈R,x2+1=0 |
| C、?x∈R,sinx<tanx |
| D、?x∈R,sinx<tanx |
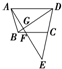 如图,梯形ABCD中,E是DC延长线上一点,AE分别交BD于G,交BC于F.则下列结论:
如图,梯形ABCD中,E是DC延长线上一点,AE分别交BD于G,交BC于F.则下列结论:①
| EC |
| CD |
| EF |
| AF |
| FG |
| AG |
| BG |
| GD |
| AE |
| AG |
| BD |
| DG |
| AF |
| CD |
| AE |
| DE |
| A、1 | B、2 | C、3 | D、4 |
已知i为虚数单位,则复数
在复平面上所对应的点在( )
| 2-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |