题目内容
以正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC，则双曲线的离心率为（ ）
A、
| ||
| B、2 | ||
C、
| ||
D、2
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC，利用正三角形的性质，结合双曲线的定义，即可求出双曲线的离心率．
解答：
解：由题意，设BC中点为D，则AB=2c，
∵正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC，
∴BD=c，AD=
c，
∴2a=（
-1）c，
∴e=
=
=
+1，
故选：C．
∵正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC，
∴BD=c，AD=
| 3 |
∴2a=（
| 3 |
∴e=
| c |
| a |
| 2 | ||
|
| 3 |
故选：C．
点评：本题考查双曲线的几何性质，考查正三角形的性质，正确理解双曲线的定义是关键．
练习册系列答案
相关题目
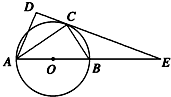如图，在△ABC和△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD，⊙O是以AB为直径的圆，DC的延长线与AB的延长线交于点E．若EB=6，EC=6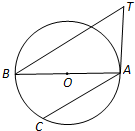
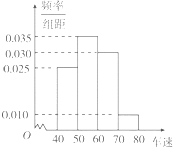市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速，为调查限速70km/h是否合理，对通过该路段的300辆汽车的车速进行检测，将所得数据按[40，50），[50，60），[60，70），[70，80）分组，绘制成如图所示的频率分布直方图．则这300辆汽车中车速低于限速的汽车有下列命题是真命题的是（ ）
| A、“若x=2，则（x-2）（x-1）=0” |
| B、“若x=0，则xy=0”的否命题 |
| C、“若x=0，则xy=0”的逆命题 |
| D、“若x＞1，则x＞2”的逆否命题 |
若（2x+1）n=a0+a1x+…+aixi+…+anxn，其中n∈N*，则a1-22a2+…+（-1）n+1n2an=（ ）
| A、（-1）n+1•2•（5n-4） |
| B、（-1）n+1•6•（3n-2） |
| C、2n（2n+1）•3n-2 |
| D、（-1）n+1•2n（2n-1） |