题目内容
已知i为虚数单位,则复数
在复平面上所对应的点在( )
| 2-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:根据复数的几何意义以及复数的基本运算即可得到结论.
解答:
解:∵
=
=
=
=
-
i,
∴复数对应的点的坐标为(
,-
),位于第四象限,
故选:D.
| 2-i |
| 1+i |
| (2-i)(1-i) |
| (1+i)(1-i) |
| 2-3i-1 |
| 2 |
| 1-3i |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴复数对应的点的坐标为(
| 1 |
| 2 |
| 3 |
| 2 |
故选:D.
点评:本题主要考查复数的几何意义以及复数的基本运算,比较基础.

练习册系列答案
相关题目
下列命题是真命题的是( )
| A、“若x=2,则(x-2)(x-1)=0” |
| B、“若x=0,则xy=0”的否命题 |
| C、“若x=0,则xy=0”的逆命题 |
| D、“若x>1,则x>2”的逆否命题 |
已知AB是⊙O的切线,在下列条件中,能判定AB⊥CD的是( )
| A、AB与⊙O相切于点C,CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C,CD过圆心 |
| D、CD也是⊙O的切线 |
已知直线2x-y+6=0过双曲线C:
-
=1(m>0)的一个焦点,则双曲线的离心率为( )
| x2 |
| m |
| y2 |
| 8 |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |

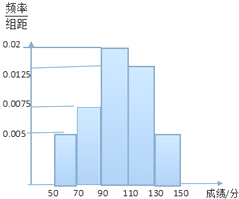 某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.
某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.