题目内容
设x+y+z=0,求证:6(x3+y3+z3)2≤(x2+y2+z2)3.
考点:不等式的证明
专题:证明题,综合法
分析:根据x+y+z=0,可得z=-(x+y),分别代入化简,结合基本不等式,即可得出结论.
解答:
证明:∵x+y+z=0,∴z=-(x+y),
∴左式=6[x3+y3-(x+y)3]2=6(3x2y+3xy2)2=54x2y2(x+y)2=27(2x2)(xy+y2)(xy+y2)
右式=[x2+y2+(x+y)2]3=(2x2+xy+y2+xy+y2)3,
∴利用基本不等式,可得(2x2+xy+y2+xy+y2)3=[(2x2)+(xy+y2)+(xy+y2)]3≥27(2x2)(xy+y2)(xy+y2),
∴右式≥左式,
∴6(x3+y3+z3)2≤(x2+y2+z2)3.
∴左式=6[x3+y3-(x+y)3]2=6(3x2y+3xy2)2=54x2y2(x+y)2=27(2x2)(xy+y2)(xy+y2)
右式=[x2+y2+(x+y)2]3=(2x2+xy+y2+xy+y2)3,
∴利用基本不等式,可得(2x2+xy+y2+xy+y2)3=[(2x2)+(xy+y2)+(xy+y2)]3≥27(2x2)(xy+y2)(xy+y2),
∴右式≥左式,
∴6(x3+y3+z3)2≤(x2+y2+z2)3.
点评:本题考查不等式的证明,考查基本不等式的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
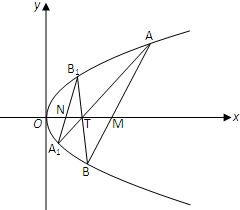 已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.
已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.