题目内容
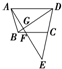如图，梯形ABCD中，E是DC延长线上一点，AE分别交BD于G，交BC于F．则下列结论：①
| EC |
| CD |
| EF |
| AF |
| FG |
| AG |
| BG |
| GD |
| AE |
| AG |
| BD |
| DG |
| AF |
| CD |
| AE |
| DE |
| A、1 | B、2 | C、3 | D、4 |
考点：相似三角形的性质
专题：立体几何
分析：利用平行线分线段成比例定理和相似三角形的性质逐个进行判断能求出正确结果．
解答：
解：∵梯形ABCD中，E是DC延长线上一点，AE分别交BD于G，交BC于F，
∴CF∥AD，
∴
=
，故①正确；
∵BF∥AD，
∴
=
，故②正确；
∵BF∥AD，
∴
=
，故③不正确；
∵CF∥AD，
∴
=
，故④正确．
故选：C．
∴CF∥AD，
∴
| EC |
| CD |
| EF |
| AF |
∵BF∥AD，
∴
| FG |
| AG |
| BG |
| GD |
∵BF∥AD，
∴
| AF |
| AG |
| BD |
| DG |
∵CF∥AD，
∴
| AF |
| CD |
| AE |
| DE |
故选：C．
点评：本题考查平行线分线段成比例定理的应用，是基础题，解题时要注意相似三角形的性质的应用．
练习册系列答案
相关题目
若（2x+1）n=a0+a1x+…+aixi+…+anxn，其中n∈N*，则a1-22a2+…+（-1）n+1n2an=（ ）
| A、（-1）n+1•2•（5n-4） |
| B、（-1）n+1•6•（3n-2） |
| C、2n（2n+1）•3n-2 |
| D、（-1）n+1•2n（2n-1） |
已知集合A={x|-2≤x≤2}，B={x|0＜x＜1}，则有（ ）
| A、A＞B | B、A?B |
| C、B?A | D、A⊆B |
把6个人平均分成两组，再从各组中分别选出正组长1名和副组长1名，则不同的选法种数是（ ）
| A、720 | B、360 |
| C、120 | D、60 |