题目内容
判断下列命题的真假,其中为真命题的是( )
| A、?x∈R,x2+1=0 |
| B、?x∈R,x2+1=0 |
| C、?x∈R,sinx<tanx |
| D、?x∈R,sinx<tanx |
考点:特称命题,命题的真假判断与应用
专题:简易逻辑
分析:利用x2非负,判断A的正误;特称命题判断B的正误;通过反例判断C的正误;利用特殊值判断D的正误;
解答:
解:对于A,∵?x∈R,x2≥0,x2+1≥1∴A不正确;
对于B,∵?x∈R,x2≥0,x2+1≥1,∴?x∈R,x2+1=0,不正确;
对于C,?x∈R,sinx<tanx,当x=-
时,sinx=-
,tanx=-1,∴sinx>tanx,∴C不正确;
对于D,当x∈(0,
),sinx<tanx,∴?x∈R,sinx<tanx,正确.
故选:D.
对于B,∵?x∈R,x2≥0,x2+1≥1,∴?x∈R,x2+1=0,不正确;
对于C,?x∈R,sinx<tanx,当x=-
| π |
| 4 |
| ||
| 2 |
对于D,当x∈(0,
| π |
| 2 |
故选:D.
点评:本题考查命题的真假的判断与应用,考查全称命题与特称命题的关系,反例是判断命题真假的有效方法之一.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列命题是真命题的是( )
| A、“若x=2,则(x-2)(x-1)=0” |
| B、“若x=0,则xy=0”的否命题 |
| C、“若x=0,则xy=0”的逆命题 |
| D、“若x>1,则x>2”的逆否命题 |
若(2x+1)n=a0+a1x+…+aixi+…+anxn,其中n∈N*,则a1-22a2+…+(-1)n+1n2an=( )
| A、(-1)n+1•2•(5n-4) |
| B、(-1)n+1•6•(3n-2) |
| C、2n(2n+1)•3n-2 |
| D、(-1)n+1•2n(2n-1) |
已知AB是⊙O的切线,在下列条件中,能判定AB⊥CD的是( )
| A、AB与⊙O相切于点C,CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C,CD过圆心 |
| D、CD也是⊙O的切线 |
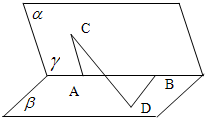 如图,在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为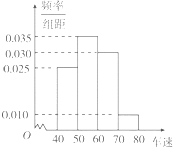 市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有
市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有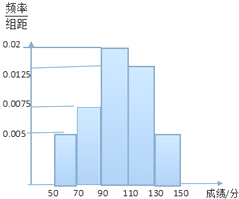 某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.
某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.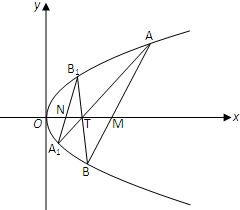 已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.
已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.