题目内容
已知点P是双曲线
-
=1上的一点(a>0),以点P及双曲线两焦点F1、F2为顶点的三角形的面积等于1,且∠F1PF2=90°,求a的值.
| x2 |
| 4a2 |
| y2 |
| a2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设|PF1|=m,|PF2|=n,根据双曲线定义得到|m-n|=4a,结合∠F1PF2=90°可得m2+n2=(2c)2=20a2,再结合以点P及双曲线两焦点F1、F2为顶点的三角形的面积等于1,即可得到结论,
解答:
解:因为P在双曲线上,设|PF1|=m,|PF2|=n,
则|m-n|=4a…(1)
由∠F1PF2=90°,可得m2+n2=(2c)2=20a2…(2)
则(1)2-(2)得:-2mn=-16a2,
∴mn=8a2,
∴直角△F1PF2的面积:S=
mn=4a2=1,
∵a>0,
∴a=
.
则|m-n|=4a…(1)
由∠F1PF2=90°,可得m2+n2=(2c)2=20a2…(2)
则(1)2-(2)得:-2mn=-16a2,
∴mn=8a2,
∴直角△F1PF2的面积:S=
| 1 |
| 2 |
∵a>0,
∴a=
| 1 |
| 2 |
点评:本题主要考查双曲线的基本性质.在涉及到与焦点有关的题目时,一般都用定义求解.

练习册系列答案
相关题目
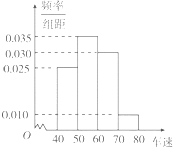 市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有
市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有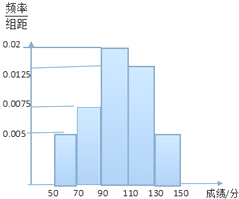 某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.
某班学生参加科普知识竞赛,成绩的频率分布直方图如图,数据的分布组依次为[50,70),[70,90),[90,110),[110,130),[130,150),已知成绩低于90分的学生人数为10人.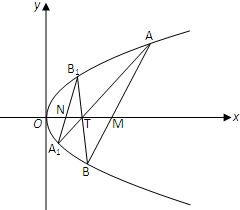 已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.
已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.