题目内容
若抛物线y2=2px的一个焦点与椭圆
+
=1的右焦点重合,
(1)求P的值;
(2)若点P(2,4)是抛物线上一点,点F为抛物线的焦点,求线段PF的长.
| x2 |
| 6 |
| y2 |
| 2 |
(1)求P的值;
(2)若点P(2,4)是抛物线上一点,点F为抛物线的焦点,求线段PF的长.
考点:直线与圆锥曲线的综合问题
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)可求抛物线的焦点坐标,即椭圆焦点坐标,从而可得
;
(2)由抛物线定义可求.
| p |
| 2 |
(2)由抛物线定义可求.
解答:
解:(1)∵椭圆
+
=1,
∴a2=6,b2=2,则c=2,
∴椭圆的右焦点坐标为(2,0),
则抛物线的焦点坐标为(2,0),
故有
=2,p=4;
(2)由(1)得:抛物线的方程为y2=8x,点P(2,4),抛物线的焦点坐标为(2,0),
由抛物线的定义得|PF|=x0+
=2+
=4.
| x2 |
| 6 |
| y2 |
| 2 |
∴a2=6,b2=2,则c=2,
∴椭圆的右焦点坐标为(2,0),
则抛物线的焦点坐标为(2,0),
故有
| p |
| 2 |
(2)由(1)得:抛物线的方程为y2=8x,点P(2,4),抛物线的焦点坐标为(2,0),
由抛物线的定义得|PF|=x0+
| p |
| 2 |
| 4 |
| 2 |
点评:该题考查抛物线的方程、性质,考查直线与抛物线的位置关系,属基础题.

练习册系列答案
相关题目
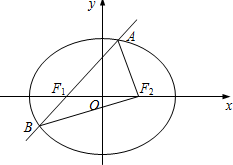 如图,椭圆E:
如图,椭圆E: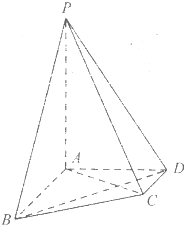 在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=
在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=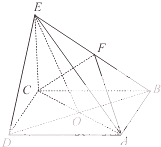 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.